Mathematik fur PharmazeutInnen . eine Einfhrung

Mathematik für PharmazeutInnen .
eine Einführung

Prof. Dr. Uli Schell
FH Kaiserslautern

1.10.2013

.
Version 5.0
© Prof. Dr. Uli Schell .
Zuletzt geändert am 16. Dezember 2013

Inhaltsverzeichnis

1 Reelle Matrizen
1.1 Einstieg: Lineare Gleichungssysteme
  1.1.1 gängige Methoden
  1.1.2 Einige Beispiele zum Einstieg
  1.1.3 Lösen von Gleichungssystemen über äquivalente Umformungen
  1.1.4 Übungen
  1.1.5 Definition einer reellen Matrix
  1.1.6 Transponierte einer Matrix
  1.1.7 Gleichheit von Matrizen
1.2 Spezielle quadratische Matrizen
  1.2.1 Diagonalmatrix
  1.2.2 Dreiecksmatrix
  1.2.3 Symmetrische Matrix
  1.2.4 Schiefsymmetrische Matrix
1.3 Rechenoperationen mit Matrizen
  1.3.1 Addition
  1.3.2 Multiplikation mit einem Skalar
  1.3.3 Multiplikation von Matrizen
  1.3.4 Übungen
1.4 Gauß’scher Algorithmus
  1.4.1 Darstellung in Matrixform
  1.4.2 Lösungsschritte des Gauß’schen Algorithmus
  1.4.3 Gauß-Jordan-Verfahren
2 Determinanten
2.1 Einstieg
  2.1.1 zweireihige Determinanten
  2.1.2 allgemeine Rechenregeln für Determinanten
2.2 Determinanten von Matrizen höherer Ordnung
  2.2.1 Dreireihige Determinanten
  2.2.2 Laplace’scher Entwicklungssatz
  2.2.3 Determinanten höherer Ordnung
  2.2.4 Lösbarkeit von Gleichungssystemen
  2.2.5 Reguläre Matrix
  2.2.6 Inverse Matrix
  2.2.7 Übungen
  2.2.8 Orthogonale Matrix
  2.2.9 Rang einer Matrix
  2.2.10 Anwendungen auf Lineare Gleichungssysteme
  2.2.11 Lösungsverhalten eines linearen (m,n)-Gleichungssystems
  2.2.12 Übungen
  2.2.13 Lösung linearer Gleichungssysteme mit der Cramer’schen Regel
  2.2.14 Auswirkungen von Rundungsfehlern
3 Anwendungen
3.1 Anwendungen in der Ökologie, Eigenwerte und Eigenvektoren
  3.1.1 Markov-Ketten und Übergangsmatrizen
  3.1.2 Leslie-Diagramme und Leslie-Matrizen
  3.1.3 Eigenwerte und Eigenvektoren
3.2 Mischungen
  3.2.1 Bestimmung von Zutatenmengen
3.3 Produktionsprozesse
  3.3.1 Matrizen zur Beschreibung von Produktionsprozessen
  3.3.2 Übungen
3.4 lineare Un-Gleichungssysteme
  3.4.1 Lineare Optimierung

1 Reelle Matrizen

1.1 Einstieg: Lineare Gleichungssysteme

1.1.1 gängige Methoden

In diesem Kapitel werden die Methoden

Gaußsches Verfahren
Gauß-Jordan-Verfahren
Cramer’sche Regel

zur Lösung von Gleichungssystemen einschließlich der Hintergründe behandelt.

1.1.2 Einige Beispiele zum Einstieg

Beispiel 1 - 1:
In der Klasse 7c sind 31 Schüler. Die Zahl der Mädchen ist um 3 kleiner als die Zahl der Jungen. Wie viele Jungen und Mädchen sind in der Klasse ?

$M$ : Mädchen		$J$ : Jungen
$M + J$	$=$	$31$
$M + 3$	$=$	$J$

Beispiel 1 - 2:
Drei Zahnräder eines Getriebes haben zusammen 80 Zähne. Bei 10 Umdrehungen des ersten Rades drehen sich das zweite 18 und das dritte 45 mal. Wie viel Zähne hat jedes Rad ?

$A + B + C$	$=$	$80$
$\frac{A}{18}$	$=$	$\frac{B}{10}$
$\frac{A}{45}$	$=$	$\frac{C}{10}$

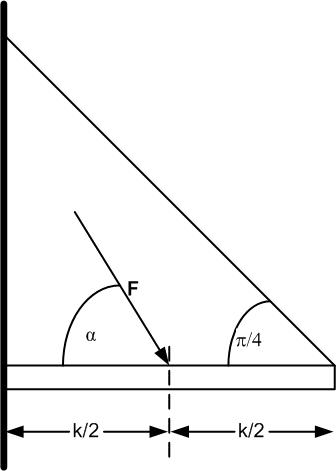
Beispiel 1 - 3: Balken in einem Lager
Ein Balken (Länge $k$ ) wird in einem festen Lager links eingespannt und rechts von einem Seil in einem Winkel von 45 o gehalten. Eine Kraft F wirkt unter dem Winkel $α$ auf die Mitte des Balkens.

Abbildung 1: Eingespannter Balken

Fragestellung der Technischen Mechanik ist bei diesem Beispiel die Bestimmung der Kräfte $F_{A}, F_{B}$ und des Moments $M_{A}$ in Abhängigkeit vom Winkel $α$ der angreifenden Kraft F (’Drehachse’ links): .

Abbildung 2: Kräfte an einem Balken

.
$\begin{matrix} x - R i c h t u n g : & 0 \cdot F_{A} & + & \frac{1}{\sqrt{2}} \cdot F_{B} & + & 0 \cdot M_{A} & = & F \cdot cos α \\ y - R i c h t u n g : & F_{A} & + & \frac{1}{\sqrt{2}} \cdot F_{B} & + & 0 \cdot M_{A} & = & F \cdot sin α \\ D r e h m o m e n t M : & 0 \cdot F_{A} & + & \frac{k}{\sqrt{2}} \cdot F_{B} & + & M_{A} & = & \frac{k}{2} \cdot F \cdot sin α \end{matrix}$ .
.
$\Rightarrow$ 3 Gleichungen, 3 Unbekannte .

Beispiel 1 - 4: Verschnittkreuz
Gegeben sind die zwei (zu bestimmenden) Mengen $x_{1}$ und $x_{2}$ eines Weins mit dem Säuregehalt $G_{1} = 3, 8 g ∕ l$ und $G_{2} = 9 g ∕ l$ , die zusammengemischt werden sollen zu einer (evtl. unbekannten) Gesamtmenge $M$ und einem Gesamtsäuregehalt $G = 6 g ∕ l$ .
Die Gleichungen dieses Systems lauten dann:

$x_{1}$	+	$x_{2}$	=	$M$
$G_{1} \cdot x_{1}$	+	$G_{2} \cdot x_{2}$	=	$G \cdot M$

Nun multipliziert man die erste Gleichung mit

G_{2}

$G_{2} \cdot x_{1}$	+	$G_{2} \cdot x_{2}$	=	$G_{2} \cdot M$
$G_{1} \cdot x_{1}$	+	$G_{2} \cdot x_{2}$	=	$G \cdot M$

Subtraktion der zweiten von der ersten Zeile ergibt:.

$(G_{2} - G_{1}) \cdot x_{1}$	+		=	$(G_{2} - G) \cdot M$

und damit

x_{1} = (G_{2} - G) \cdot \frac{M}{G_{2} - G_{1}}

oder $x_{1} \propto G_{2} - G$
Die gleichen Schritte werden nach der Multiplikation der ersten Gleichung mit $G_{1}$ analog durchgeführt:

$G_{1} \cdot x_{1}$	+	$G_{1} \cdot x_{2}$	=	$G_{1} \cdot M$
$G_{1} \cdot x_{1}$	+	$G_{2} \cdot x_{2}$	=	$G \cdot M$

Subtraktion der zweiten von der ersten Zeile ergibt:.

	+	$(G_{2} - G_{1}) \cdot x_{2}$	=	$(G - G_{1}) \cdot M$

und damit

x_{2} = (G - G_{1}) \cdot \frac{M}{G_{2} - G_{1}}

oder

x_{2} \propto G - G_{1}

.
Kennt man die gesuchte Gesamtmenge nicht, kann man für das Verhältnis von

x_{1}

x_{2}

angeben:

\frac{x_{1}}{x_{2}} = \frac{G_{2} - G}{G - G_{1}} = \frac{(9.0 - 6.0) g ∕ l}{(6.0 - 3.8) g ∕ l} = \frac{3.0}{2.2} \approx 1.36

Zum besseren Behalten dieser Gleichungen werden die Werte in einem (Verschnitt-)Kreuz aufgetragen:


$G_{1}$		$x_{1} \propto (G_{2} - G)$
	$G$
$G_{2}$		$x_{2} \propto (G - G_{1})$

.
.
Mit Zahlen: .
.



$3.8$		$3.0$
	$6.0$
$9.0$		$2.2$

.
.
Hat man nun eine vorgegebene Menge

x_{1} = 630 l

, so kann man die Menge des Weins

x_{2}

einfach bestimmen zu:

\frac{630}{x_{2}} = \frac{3.0}{2.2}

und

x_{2} = \frac{630 \cdot 2.2}{3.0} l = 462 l

.
Lösung des Beispiels mit Maple:
restart; eq1 := x1+x2 = M;
eq2 := 3.8*x1+9*x2 = 6.0*M;
solve({eq1, eq2}, {x1, x2,M}) ergibt:
x1 + x2 = M
3.8 x1 + 9 x2 = 6.0 M
{M = 2.363636364*x2, x1 = 1.363636364*x2, x2 = x2}.
Also: $x_{2}$ ist frei wählbar, daraus ergibt sich $x_{1}$ und daraus wiederum die Gesamtmenge.

Beispiel 1 - 5 mt9001
Gegeben sind die drei (zu bestimmenden) Mengen $x_{1}$ , $x_{2}$ und $x_{3}$ eines Weins mit dem Alkoholgehalt $A_{1} = 8$ Vol %, $A_{2} = 12$ Vol % und $A_{3} = 15$ Vol % , die zusammengemischt werden sollen zu einer (evtl. unbekannten) Gesamtmenge $M$ und einem Gesamt-Alkoholgehalt $A = 12$ Vol %.
(1.267 l Alkohol entspricht 1 kg; auf der linken und rechten Seite steht aber der gleiche Faktor.)
Gleichzeitig haben die Weine Säuregehalte von $S_{1} = 3 g ∕ l$ , $S_{2} = 9 g ∕ l$ und $S_{3} = 5 g ∕ l$ ,die zusammengemischt den Ziel-Gesamtsäuregehalt $G = 6 g ∕ l$ haben sollen. .
.

PICT .

Beispiel 1 - 6 mt9002
Gegeben sind die drei (zu bestimmenden) Mengen $x_{1}$ , $x_{2}$ und $x_{3}$ eines Weins mit dem Alkoholgehalt $A_{1} = 8$ Vol %, $A_{2} = 12$ Vol % und $A_{3} = 13, 5$ Vol % , die zusammengemischt werden sollen zu einer (evtl. unbekannten) Gesamtmenge $M$ und einem Gesamt-Alkoholgehalt $A = 12$ Vol %.
(1.267 l Alkohol entspricht 1 kg; auf der linken und rechten Seite steht aber der gleiche Faktor.)
Gleichzeitig haben die Weine Säuregehalte von $S_{1} = 3, 8 g ∕ l$ , $S_{2} = 9 g ∕ l$ und $S_{3} = 7 g ∕ l$ ,die zusammengemischt den Ziel-Gesamtsäuregehalt $G = 6 g ∕ l$ haben sollen. .
.

PICT .

Die Systematik von linearen Gleichungssytemen kann diese Ergebnisse erklären.

1.1.3 Lösen von Gleichungssystemen über äquivalente Umformungen

Die Lösungsmenge eines linearen Gleichungssystem s $A \vec{x} = \vec{c}$ bleibt bei Anwendung der folgenden Operationen unverändert erhalten (Äquivalente Umformungen eines linearen Gleichungssystems):

1.: Zwei Zeilen können miteinander vertauscht werden.
2.: Jede Gleichung kann mit einer von Null verschiedenen Zahl multipliziert werden.
3.: Zu jeder Gleichung darf ein Vielfaches einer anderen Gleichung addiert werden.

.
Beispiel 1 - 7 mt9003 .

					Zeilen-	Opera-
					summe	tion
$- x$	$+ y$	$+ z$	$=$	$0$	$1$
$x$	$- 3 y$	$- 2 z$	$=$	$5$	$1$	+I
$5 x$	$+ y$	$+ 4 z$	$=$	$3$	$13$	+ 5I

.

Lösungsansatz: Bringe Gleichungssystem auf Dreiecksform

.
.
.

PICT .

$\to$ Gauß’scher Algorithmus : Bringe das Gleichungssystem durch geeignete äquivalente Umformungen in Dreiecksform. Die letzte Zeile enthält die Lösung für eine Variable. Diese Lösung wird in der zweitletzten Zeile zur Bestimmung der zweiten Variablen verwendet usw.
Eine gebräuchliche Darstellungsform des Gleichungssystems ist die Matrixform

1.1.4 Übungen

1.1.5 Definition einer reellen Matrix

Matrix :	rechteckiges Schema mit
	$m$ Zeilen
	$n$ Spalten
$a_{i k}$ :	Matrixelemente

(\begin{matrix} a_{11} & a_{12} & … & a_{1 n} \\ a_{21} & a_{22} & … & a_{2 n} \\ ⋮ & ⋮ & ⋮ \\ a_{m 1} & a_{m 2} & … & a_{m n} \end{matrix})

.

i wird als Zeilenindex
k wird als Spaltenindex bezeichnet.

Schreibweisen:

A, A_{(m, n)}, a_{i k}, {(a_{i k})}_{m, n}

Sonderfälle:

$m = n$ : n-reihige quadratische Matrix oder auch Matrix n-ter Ordnung .
Nullmatrix $0$ : Matrix, deren Elemente sämtlich verschwinden .

Spaltenmatrix: $(\begin{matrix} a_{1} \\ a_{2} \\ ⋮ \\ a_{n} \end{matrix})$
.

Zeilenmatrix: $(\begin{matrix} a_{1} & a_{2} & … & a_{n} \end{matrix})$ .

1.1.6 Transponierte einer Matrix

Vertauschen von Zeilen und Spalten ergibt die Transponierte einer Matrix : $a_{i k}^{T} = a_{k i}$ .
Beispiel:
$A = (\begin{matrix} 1 & 3 \\ 4 & 2 \\ 0 & - 8 \end{matrix}) \Rightarrow A^{T} = (\begin{matrix} 1 & 4 & 0 \\ 3 & 2 & - 8 \end{matrix})$ .
.
Beispiel 1 - 8

$B = (\begin{matrix} 1 & 1 & 1 \\ 0 & - 2 & 5 \\ 7 & 6 & 0 \end{matrix}) B^{T} =$ .
.
.
.

$(\begin{matrix} ⋆ & ⋆ & ⋆ \\ ⋆ & ⋆ & ⋆ \\ ⋆ & ⋆ & ⋆ \\ ↗ & ↖ \end{matrix})$
.
.
$↗$ = Nebendiagonale
$↖$ = Hauptdiagonale

1.1.7 Gleichheit von Matrizen

Zwei Matrizen $A, B$ sind gleich, wenn
$a_{i k} = b_{i k}$ für alle $i, k$ ,
also wenn alle ihre Elemente gleich sind.

1.2 Spezielle quadratische Matrizen

1.2.1 Diagonalmatrix

$a_{i k} = 0$ für $i \neq k$

$(\begin{matrix} a_{11} & 0 & 0 & … & 0 \\ 0 & a_{22} & 0 & … & 0 \\ 0 & 0 & a_{33} & … & 0 \\ ⋮ & ⋮ & ⋮ & \dots & ⋮ \\ 0 & 0 & 0 & … & a_{n n} \end{matrix})$
.

Sind alle $a_{i i} = 1$ , so nennt man diese Matrix Einheitsmatrix

$(\begin{matrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{matrix}) = E$ .

1.2.2 Dreiecksmatrix

alle Elemente oberhalb oder unterhalb der Hauptdiagonalen verschwinden

Untere Dreiecksmatrix: $a_{i k} = 0$ für $k > i$
Obere Dreiecksmatrix: $a_{i k} = 0$ für $k < i$

Beispiel 1 - 9: Untere Dreieicksmatrix:
$(\begin{matrix} 1 & 0 & 0 \\ 3 & 1 & 0 \\ 4 & 0 & 5 \end{matrix})$
.

1.2.3 Symmetrische Matrix

$a_{i k} = a_{k i}$ $A^{T} = A$ .
Beispiel:

$(\begin{matrix} 1 & 4 & - 2 \\ 4 & 5 & 0 \\ - 2 & 0 & 8 \end{matrix})$ .

1.2.4 Schiefsymmetrische Matrix

$a_{i k} = - a_{k i}$ $\Rightarrow a_{i i} = 0$ .
Beispiel: .
$(\begin{matrix} 0 & 4 & 3 \\ - 4 & 0 & - 5 \\ - 3 & 5 & 0 \end{matrix})$ .

1.3 Rechenoperationen mit Matrizen

1.3.1 Addition

$C = A + B \Rightarrow c_{i k} = a_{i k} + b_{i k}$
.
Beispiel 1 - 10 mt9005 .
$A = (\begin{matrix} 1 & 5 & - 3 \\ 4 & 0 & 8 \end{matrix}) + B = (\begin{matrix} 5 & 1 & 3 \\ - 1 & 4 & 7 \end{matrix})$ .

.
.
.

PICT .

.
Beispiel 1 - 11: - - -- -T
-C -=- A + <msup><mrow>B< /mrow><mrow ></mrow></msup > .
Diese Operation ist nicht definiert .

1.3.2 Multiplikation mit einem Skalar

$λ \cdot A = λ \cdot (a_{i k}) = (λ \cdot a_{i k})$ für alle $i, k$ .
.
Beispiel 1 - 12 mt9006 .
$A = (\begin{matrix} 1 & - 5 & 3 \\ 4 & 1 & 0 \end{matrix}), λ = 4 B = λ \cdot A =$ .

.
.
.

PICT .

kommutativ:	$A + B$	$=$	$B + A$
	$λ \cdot A$	$=$	$A \cdot λ$
assoziativ:	$A + (B + C)$	$=$	$(A + B) + C$
	$λ \cdot (μ \cdot A)$	$=$	$(λ \cdot μ) \cdot A$
distributiv:	$(λ + μ) A$	$=$	$λ A + μ A$
	$λ (A + B)$	$=$	$λ A + λ B$

Beispiel 1 - 13 mt9007

$A = (\begin{matrix} 1 & 3 \\ 2 & 4 \end{matrix}), C = (\begin{matrix} 0 & 2 \\ 1 & 3 \end{matrix})$ .
$B = 3 \cdot A + C^{T} =$

.
.
.

PICT .

1.3.3 Multiplikation von Matrizen

$A = (\begin{matrix} 1 & 5 \\ 2 & 3 \end{matrix})$ und $B = (\begin{matrix} 4 & 1 & 2 \\ 1 & 0 & 3 \end{matrix})$

$C = A \cdot B$
.

Die Ergebnismatrix hat 3 Spalten und 2 Zeilen

$C = (\begin{matrix} c_{11} & c_{12} & c_{13} \\ c_{21} & c_{22} & c_{23} \end{matrix})$
.

$c_{11} = a_{11} \cdot b_{11} + a_{12} \cdot b_{21} = 1 \cdot 4 + 5 \cdot 1 = 9$

Falk-Schema für die Multiplikation von Matrizen : .
.

$A = (\begin{matrix} 1 & 5 \\ 2 & 3 \end{matrix})$	$C$

	$B = (\begin{matrix} 4 & 1 & 2 \\ 1 & 0 & 3 \end{matrix})$


$a_{11}$	$a_{12}$	$c_{11}$	$c_{12}$	$c_{13}$

$a_{21}$	$a_{22}$	$c_{21}$	$c_{22}$	$c_{23}$


		$b_{11}$	$b_{12}$	$b_{13}$

		$b_{21}$	$b_{22}$	$b_{23}$

C = A \cdot B

$c_{i k}$	$=$	$a_{i 1} \cdot b_{1 k} + a_{i 2} \cdot b_{2 k} + \dots + a_{i n} \cdot b_{n k}$
	$=$	$\sum_{j = 1}^{n} a_{i j} \cdot b_{j k}$

Beispiel 1 - 14:
$A = (\begin{matrix} 1 & 4 & 2 \\ 4 & 0 & - 3 \end{matrix}) B = (\begin{matrix} 1 & 1 & 0 \\ - 2 & 3 & 5 \\ 0 & 1 & 4 \end{matrix})$

C = A \cdot B


$1$	$4$	$2$	$- 7$	$15$	$28$

$4$	$0$	$- 3$	$4$	$1$	$- 12$


			$1$	$1$	$0$

			$- 2$	$3$	$5$

			$0$	$1$	$4$

Multiplikation ist nur zulässig, wenn $Spaltenanzahl A = Zeilenanzahl B$ .

Beispiel 1 - 15 mt9008
$A = (\begin{matrix} 1 & - 5 & 3 \\ 4 & 1 & 0 \end{matrix}), B = (\begin{matrix} 1 & 0 \\ 1 & 0 \\ 1 & 2 \end{matrix})$ .
.
$A \cdot B =$ .

.
.

PICT .

Rechengesetze für die Matrixmultiplkikation:

Assoziativität:	$A \cdot (B \cdot C)$	$=$	$(A \cdot B) \cdot C$
Distributivität:	$A \cdot (B + C)$	$=$	$A \cdot B + A \cdot C$
	$(A + B) \cdot C$	$=$	$A \cdot C + B \cdot C$
	${(A \cdot B)}^{T}$	$=$	$B^{T} \cdot A^{T}$
	$A \cdot E$	$=$	$E \cdot A = A$

Die Matrixmultiplikation ist nicht kommutativ

Man kann jedoch bei Gleichungen mit Matrizen entweder auf beiden Seiten von links oder auf beiden Seiten von rechts mit einer Matrix multiplizieren (vorausgesetzt natürlich, die Anzahl Spalten bzw. Zeilen sind dazu passend): .

	$(B \cdot C)$	$=$	$(E \cdot F)$
$\to$	$A \cdot (B \cdot C)$	$=$	$A \cdot (E \cdot F)$
$\to$	$(B \cdot C) \cdot A$	$=$	$(E \cdot F) \cdot A$

1.3.4 Übungen

1.4 Gauß’scher Algorithmus

1.4.1 Darstellung in Matrixform

$- x$	$+ y$	$+ z$	$=$	$0$			umbilden in Matrix:
$x$	$- 3 y$	$- 2 z$	$=$	$5$	$\Rightarrow$	1. Spalte: $x$ ,	2. Spalte: $y$
$5 x$	$+ y$	$+ 4 z$	$=$	$3$		3. Spalte: $z$ ,	4. Spalte: Konstante

$\Rightarrow$

$- 1$	$+ 1$	$+ 1$	$0$
$1$	$- 3$	$- 2$	$5$
$5$	$1$	$4$	$3$

.
Das lineare Gleichungssystem kann geschrieben werden als $A \cdot \vec{x} = \vec{c}$ .
nz Koeffizienten: $a_{i k}$
Absolutglieder (Konstanten): $c_{i}$

$A \cdot \vec{x} = \vec{c} \Rightarrow$

$a_{11} \cdot x_{1}$	$+ a_{12} \cdot x_{2}$	$+ a_{13} \cdot x_{3}$	$+ \dots$	$+ a_{1 n} \cdot x_{n}$	$=$	$c_{1}$
$a_{21} \cdot x_{1}$	$+ a_{22} \cdot x_{2}$	$+ a_{23} \cdot x_{3}$	$+ \dots$	$+ a_{2 n} \cdot x_{n}$	$=$	$c_{2}$
$a_{31} \cdot x_{1}$	$+ a_{32} \cdot x_{2}$	$+ a_{33} \cdot x_{3}$	$+ \dots$	$+ a_{3 n} \cdot x_{n}$	$=$	$c_{3}$
$⋮$	$⋮$	$⋮$	$⋮$ $⋮$ $⋮$	$⋮$		$⋮$

$\Rightarrow$	$A \cdot \vec{x}$	$=$	$\vec{c}$	mit $\vec{x} = (\begin{matrix} x_{1} \\ x_{2} \\ x_{3} \\ ⋮ \end{matrix})$	und $\vec{c} = (\begin{matrix} c_{1} \\ c_{2} \\ c_{3} \\ ⋮ \end{matrix})$

Entsprechend verfolgt jetzt der Gaußsche Algorithmus das Ziel, über äquivalente Umformungen die Matrix $A$ in ein gestaffeltes System (Dreiecksform) zu bringen durch die Schritte:

1.: Vertauschen von Zeilen
2.: Multiplikation mit einem Faktor $\neq 0$
3.: Addition eines Vielfachen einer anderen Zeile

.
Beispiel 1 - 16 mt9026 .
Lösen eines Gleichungssytems mit Excel : .

Abbildung 3: Gleichungssystem als Excel-Tabelle

.
.

.
.
.

PICT .

.
Beispiel 1 - 17 mt9009 .
Lösung des obigen Beispiels: .

$- x$	$+ y$	$+ z$	$=$	$0$			umbilden in Matrix:
$x$	$- 3 y$	$- 2 z$	$=$	$5$	$\Rightarrow$	1. Spalte: $x$ ,	2. Spalte: $y$
$5 x$	$+ y$	$+ 4 z$	$=$	$3$		3. Spalte: $z$ ,	4. Spalte: Konstante

.
.
.

PICT .

1.4.2 Lösungsschritte des Gauß’schen Algorithmus

Die Lösung eines linearen Gleichungssystems $A \cdot \vec{x} = \vec{c}$ erfolgt durch Umformung in zwei, ggf. drei Schritten:
I. Vorwärtselimination mit
Ia. eventueller Pivotisierung (d.h. Vertauschen von Zeilen, bis die Diagonalelemente $\neq 0$ )
II. Rückwärtselimination

I. Vorwärtselimination

1.

Eliminationsschritt: (

a_{11} \neq 0

)

subtrahiere	$a_{21} ∕ a_{11}$ -fache der 1.Zeile von 2.Zeile
⋮	$a_{31} ∕ a_{11}$ -fache der 1.Zeile von 3.Zeile
⋮	⋮

Durch den ersten Eliminationsschritt entstehen in der 1. Spalte der Matrix Nullen, außer

a_{1} 1

sind alle

a_{i} 1 = 0

2.

Eliminationsschritt: (

a_{22} \neq 0

)

subtrahiere	$a_{32} ∕ a_{22}$ -fache der 2.Zeile von 3.Zeile
⋮	$a_{42} ∕ a_{22}$ -fache der 2.Zeile von 4.Zeile
⋮	⋮

3.

Solange wiederholen, bis die Dreiecksform vorliegt. (Die Koeffizienten der Matrix in Dreiecksform werden ab hier der Übersichtlichkeit halber mit Koeffizienten

{a^{'}}_{i k}

bzw.

{c^{'}}_{i}

bezeichnet.)

Ia. Pivotisierung

1.: Das Gauß-Verfahren versagt, falls das Diagonalelement oder Pivotelement (engl. für Dreh- und Angelpunkt) $a_{k k}$ eines Eliminationsschrittes gleich Null ist, $a_{k k} = 0$ (Abbruch des Verfahrens bei Division durch Null).
2.: Pivotsuche: Ist ein Diagonalelement $a_{k k} = 0$ , so vertauscht man die Pivot-Zeile k vor Ausführung des k-ten Eliminationsschrittes mit derjenigen Zeile $m > k$ , die den betragsmäßig größten Koeffizienten für $x_{k}$ besitzt:
3.: Neue Pivotzeile $m$ , neues Pivotelement $a_{m k}$ .

II. Rückwärtselimination
Aus der Dreiecksform werden die Lösungen $x_{i}$ durch schrittweises Rückwärtseinsetzen gewonnen:

1.: Zuerst die unterste Zeile nach $x_{n}$ auflösen.
2.: Die anderen Elemente $x_{i}, i = n - 1, \dots, 1$ des Lösungsvektors $x$ bestimmt man dann rekursiv mit der Gleichung $x_{n} =$ $\frac{{c^{'}}_{n}}{{a^{'}}_{n n}}$ , $x_{i} = \frac{{c^{'}}_{i}}{{a^{'}}_{i i}} - \sum_{k = i + 1}^{n} x_{k} \cdot \frac{{a^{'}}_{i k}}{{a^{'}}_{i i}}, i = n - 1, \dots, 1$

.
Sei $A$ eine $4 x 4$ -Matrix, dann lautet das Gleichungssystem $A \cdot \vec{x} = \vec{c}$ mit dem unbekannten Vektor $\vec{x} = {(x_{-} 1, x_{2}, \dots x_{n})}^{T}$ :

$a_{11} x_{1}$	$+$	$a_{12} x_{2}$	$+$	$a_{13} x_{3}$	$+$	$a_{14} x_{4}$	$=$	$c_{1}$
		$a_{22} x_{2}$	$+$	$a_{23} x_{3}$	$+$	$a_{24} x_{4}$	$=$	$c_{2}$
				$a_{33} x_{3}$	$+$	$a_{34} x_{4}$	$=$	$c_{3}$
						$a_{44} x_{4}$	$=$	$c_{4}$

x_{4}

erhält man aus der letzten Zeile:

x_{4} = \frac{c_{4}}{a_{44}}

Der Wert für

x_{4}

wird in die vorletzte Zeile eingesetzt, diese nach

x_{3}

aufgelöst:

x_{3} = \frac{c_{3} - a_{34} x_{4}}{a_{33}}

.
.
Das gleiche Schema wird auf die darüberliegenden Zeilen angewandt, bis alle Werte von

\vec{x}

bestimmt sind.

1.4.3 Gauß-Jordan-Verfahren

Alternativ zum beschriebenen Gauß-Verfahren kann man auch die Koeffizientenmatrix noch weiter umformen, bis man eine Einheitsmatrix $E$ erhält. Damit können die Lösungen direkt abgelesen werden.

$A \cdot \vec{x} = \vec{c}$
$A^{- 1} \cdot A \cdot \vec{x} = A^{- 1} \cdot \vec{c}$ oder
$\vec{x} = A^{- 1} \cdot \vec{c}$
Dies ist auch als Gauß-Jordan-Verfahren bekannt.
.
Beispiel 1 - 18 mt9025 .
Alternative Lösung des obigen Beispiels mit Gauß-Jordan: .

$- x$	$+ y$	$+ z$	$=$	$0$			umbilden in Matrix:
$x$	$- 3 y$	$- 2 z$	$=$	$5$	$\Rightarrow$	1. Spalte: $x$ ,	2. Spalte: $y$
$5 x$	$+ y$	$+ 4 z$	$=$	$3$		3. Spalte: $z$ ,	4. Spalte: Absolutglied

.
(Anm.: Man kann das Absolutglied zuerst auch auf die linke Seite der Gleichung bringen, man muß nur beim Ablesen darauf achten.) .
.
.

PICT .

.
Beispiel 1 - 19 mt9010 .
Zu lösen ist das Gleichungssystem .

$- x$	$+ y$	$- z$	$=$	$- 2$
	$+ y$	$- 2 z$	$=$	$- 4$
		$- z$	$=$	$- 15$

.
.
.

PICT .

Beispiele zum Gauß’schen Verfahren
.
Beispiel 1 - 20 mt9011 .
Tragwerke

$F_{A}$	$F_{B}$	$M_{A}$	$c$
$0$	$\frac{1}{\sqrt{2}}$	$0$	$F cos α$	nach $I I$
$1$	$\frac{1}{\sqrt{2}}$	$0$	$F sin α$	nach $I$
$0$	$\frac{k}{\sqrt{2}}$	$1$	$\frac{k}{2} \cdot F sin α$

.
Pivotisieren:

.
.
.

PICT .

.
Beispiel 1 - 21 mt9012 .

(\begin{matrix} 1 & 1 & - 2 \\ 1 & - 1 & - 2 \\ 2 & 3 & - 4 \end{matrix}) \cdot (\begin{matrix} x \\ y \\ z \end{matrix}) = (\begin{matrix} 0 \\ 0 \\ 0 \end{matrix})

$1$	$1$	$- 2$	$0$
$1$	$- 1$	$- 2$	$0$
$2$	$3$	$- 4$	$0$

.
.
.
.

PICT .

.
Beispiel 1 - 22 mt9013 .

$- x_{1}$	$+ 2 x_{2}$	$+ x_{3}$	$=$	$6$
$x_{1}$	$+ x_{2}$	$+ x_{3}$	$=$	$- 2$
$2 x_{1}$	$- 4 x_{2}$	$- 2 x_{3}$	$=$	$- 6$

.
.
.

PICT .

Ein Gleichungssystem hat

$\}$

eine oder keine oder unendlich viele

Lösungen. .

Ist das Gleichungssystem (

\vec{c} = 0

) homogen, so hat es entweder genau eine Lösung (die Triviallösung

\vec{x} = \vec{0}

) oder unendlich viele Lösungen (darunter auch die Triviallösung).

2 Determinanten

2.1 Einstieg

2.1.1 zweireihige Determinanten

$2 \times 2$ Gleichungssysteme $A \cdot \vec{x} = \vec{c}$ können wie folgt umgeformt werden:

$a_{11} x_{1}$	$+ a_{12} x_{2}$	$=$	$c_{1}$	$\cdot a_{22}$
$a_{21} x_{1}$	$+ a_{22} x_{2}$	$=$	$c_{2}$	$\cdot (- a_{12})$

\}

a11a22 ⋅ x1 +a12a22 ⋅ x2= c1 ⋅ a22 -a12a21 ⋅ x1-a12a22 ⋅ x2=-c2 ⋅ a12

\Rightarrow

a_{11} a_{22} \cdot x_{1} - a_{12} a_{21} \cdot x_{1} = c_{1} \cdot a_{22} - c_{2} \cdot a_{12}

(a_{11} a_{22} - a_{12} a_{21}) x_{1} = c_{1} \cdot a_{22} - c_{2} \cdot a_{12}

\Rightarrow x_{1} = \frac{c_{1} \cdot a_{22} - c_{2} \cdot a_{12}}{a_{11} a_{22} - a_{12} a_{21}}

, analog:

\Rightarrow x_{2} = \frac{c_{2} \cdot a_{11} - c_{1} \cdot a_{21}}{a_{11} a_{22} - a_{12} a_{21}} \Rightarrow

Beide Nenner sind gleich.
.
Bildet man aus der Koeffizientenmatrix

$A = (\begin{matrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{matrix})$ den Wert $D = a_{11} \cdot a_{22} - a_{21} \cdot a_{12}$ ,
.
hat man die Koeffizientendeterminante der Matrix $A$ bestimmt.
Da die Koeffizientenmatrix eine $2 x 2$ -Matrix ist, spricht man von einer 2-reihigen Koeffizientendeterminanten oder Koeffizientendeterminanten 2. Ordnung.

Ist der Wert der Determinanten $D = 0$ , so hat das Gleichungssystem keine (bzw. bei einem homogenen Gleichungssystem unendlich viele) Lösung(en).
Determinanten lassen sich nur für quadratische Matrizen (d.h. die Matrix hat genau so viele Zeilen wie Spalten) angeben.

Rechenregel zur Bestimmung einer $2 x 2$ -Determinanten:

$D = det A = |\begin{matrix} a_{11} & a_{12} \\ \times \\ a_{21} & a_{22} \end{matrix}| = | A | = | a_{i k} |$
.

Die Determinante erhält man, indem man das Produkt der Hauptdiagonal-Elemente bildet und davon das Produkt der Nebendiagonal-Elemente subtrahiert:

$det A = det (\begin{matrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{matrix}) = a_{11} \cdot a_{22} - a_{21} \cdot a_{12}$
.
Beispiel 2 - 23:

$det A = |\begin{matrix} 5 & 3 \\ - 10 & - 6 \end{matrix}| = - 30 + 30 = 0$ .

.
Beispiel 2 - 24 mt9014 .

1.: $det A = |\begin{matrix} 3 & 5 \\ - 2 & - 4 \end{matrix}| =$
2.: $det A = |\begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix}| =$
3.: $det A = |\begin{matrix} 5 & 3 \\ - 10 & - 6 \end{matrix}| =$

.
.
.
.

PICT .

2.1.2 allgemeine Rechenregeln für Determinanten

Die hier aufgeführten Rechenregeln gelten auch für Determinanten höherer Ordnung:

1.

Der Wert einer Determinante ändert sich nicht, wenn man Zeilen und Spalten vertauscht

2.

Beim Vertauschen zweier Zeilen (bzw. Spalten) ändert sich das Vorzeichen

3.

Multlipliziert man eine Zeile (bzw Spalte) mit

λ

, dann multipliziert sich die Determinante
mit

λ

4.

Eine Determinante besitzt den Wert

0

, wenn

(a): alle Elemente einer Zeile (oder Spalte) Null sind
(b): Zwei Zeilen (oder Spalten) gleich sind
(c): Zwei Zeilen (oder Spalten) zueinander proportional sind
(d): Eine Zeile (oder Spalte) als Linearkombination der übrigen Zeilen (oder Spalten) darstellbar ist.

5.

Der Wert einer Determinante ändert sich nicht, wenn man zu einer Zeile (oder Spalte) das Vielfache einer anderen Zeile (oder Spalte) addiert.

6.

det (A \cdot B) = det A \cdot det B

7.

Dreiecksmatrizen

$A_{\prod} = (\begin{matrix} a_{11} & a_{12} & a_{13} & \dots \\ 0 & a_{22} & a_{23} & \dots \\ 0 & 0 & a_{33} & \dots \\ ⋮ & ⋮ & ⋮ & \dots \end{matrix})$
.

haben als Determinante das Produkt der Hauptdiagonalen
$det A_{\prod} = a_{11} \cdot a_{22} \cdot a_{33} \cdot \dots = \overset{i}{\propto} a_{i i}$

Beispiel 2 - 25:

1.

Der Wert einer Determinante ändert sich nicht, wenn man Zeilen und Spalten vertauscht: .

$det A^{T} = det A$

$det A = |\begin{matrix} 8 & 5 \\ - 3 & 2 \end{matrix}| = 16 + 15 = 31$
$det A^{T} = |\begin{matrix} 8 & - 3 \\ 5 & 2 \end{matrix}| = 16 + 15 = 31$
.

2.

Beim Vertauschen zweier Zeilen (bzw. Spalten) ändert sich das Vorzeichen: .

$det A = |\begin{matrix} 7 & 3 \\ 4 & - 1 \end{matrix}| = - 7 - 12 = - 19$

$det A^{'} = |\begin{matrix} 4 & - 1 \\ 7 & 3 \end{matrix}| = 12 + 7 = 19$ .

3.

Multlipliziert man eine Zeile (bzw Spalte) mit

λ

, dann multipliziert sich die Determinante
mit

λ

: .

det A = |\begin{matrix} 2 \cdot 5 & 2 \cdot 5 \\ - 3 & 2 \end{matrix}| = 20 + 30 = 50 = 2 \cdot 25 = 2 \cdot |\begin{matrix} 5 & 5 \\ - 3 & 2 \end{matrix}|

⨳¡

.
(Achtung! Nicht verwechseln mit der Skalarmultiplikation bei Matrizen!)

4.

Eine Determinante besitzt den Wert

0

, wenn

(a): alle Elemente einer Zeile (oder Spalte) Null sind
(b): Zwei Zeilen (oder Spalten) gleich sind
(c): Zwei Zeilen (oder Spalten) zueinander proportional sind
(d): Eine Zeile (oder Spalte) als Linearkombination der übrigen Zeilen (oder Spalten) darstellbar ist: .

$det A = \|\begin{matrix} 1 & 5 \\ 0 & 0 \end{matrix}\| = 0$		$det B = \|\begin{matrix} 4 & 3 \\ 4 & 3 \end{matrix}\| = 0$		$det C = \|\begin{matrix} 4 & 2 \\ 8 & 4 \end{matrix}\| = 0$

5.

Der Wert einer Determinante ändert sich nicht, wenn man zu einer Zeile (oder Spalte) das Vielfache einer anderen Zeile (oder Spalte) addiert: .

$det A = |\begin{matrix} - 6 & 5 \\ 1 & 4 \end{matrix}| = - 24 - 5 = - 29$

Addition des 6-fachen von Zeile II zu Zeile I:

$det A = |\begin{matrix} 0 & 29 \\ 1 & 4 \end{matrix}| = 0 - 29 = - 29$
.

6.

$det (A \cdot B) = det A \cdot det B$ .

$A = (\begin{matrix} 1 & 4 \\ 5 & - 2 \end{matrix})$		$B = (\begin{matrix} - 2 & - 3 \\ 4 & 1 \end{matrix})$

det A \cdot det B = (- 22) \cdot (10) = - 220

det (A \cdot B) = |\begin{matrix} 14 & 1 \\ - 18 & - 17 \end{matrix}| = - 220

7.

Dreiecksmatrizen haben als Determinante das Produkt der Hauptdiagonalen

$det A_{\prod} = a_{11} \cdot a_{22} \cdot a_{33} \cdot \dots = \overset{i}{\propto} a_{i i}$ : .

$det A = |\begin{matrix} 5 & - 4 \\ 0 & - 3 \end{matrix}| = 5 \cdot (- 3) - 0 \cdot (- 4) = 5 \cdot (- 3) = - 15$

2.2 Determinanten von Matrizen höherer Ordnung

2.2.1 Dreireihige Determinanten

Beispiel 2 - 26:
Gegeben sei ein $3 \times 3$ Gleichungssystem $A \cdot \vec{x} = \vec{c}$ ,
ausgeschrieben:

$a_{11} x_{1}$	$+ a_{12} x_{2}$	$+ a_{13} x_{3}$	$=$	$c_{1}$
$a_{21} x_{1}$	$+ a_{22} x_{2}$	$+ a_{23} x_{3}$	$=$	$c_{2}$
$a_{31} x_{1}$	$+ a_{32} x_{2}$	$+ a_{33} x_{3}$	$=$	$c_{3}$

Bildet man aus der Koeffizientenmatrix

A = (\begin{matrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{matrix})

.
den Term

$D$	$=$	$a_{11} \cdot a_{22} \cdot a_{33}$	$+$	$a_{12} \cdot a_{23} \cdot a_{31}$	$+$	$a_{13} \cdot a_{21} \cdot a_{32}$	$-$
	$-$	$a_{13} \cdot a_{22} \cdot a_{31}$	$-$	$a_{11} \cdot a_{23} \cdot a_{32}$	$-$	$a_{12} \cdot a_{21} \cdot a_{33}$	,

hat man die Koeffizientendeterminante der Matrix

A

bestimmt.
Ist der Wert der Determinanten

D = 0

, so hat das Gleichungssystem keine (oder unendlich viele) Lösung(en).
Schreibweisen:

$D = det A = |\begin{matrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{matrix}| = | A | = | a_{i k} |$
.

Man spricht hier von dreireihigen Determinanten oder Determinanten 3. Ordnung.

Als Merkregel für die Bestimmung der dreireihigen Determinante von $A$ kann man die Regel von Sarrus verwenden, indem man das Produkt der Hauptdiagonalen addiert und das Produkt der Nebendiagonalen subtrahiert:
( $↗$ = Nebendiagonale, $↖$ = Hauptdiagonale)

$D = det A = |\begin{matrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{matrix}| \begin{matrix} a_{11} & a_{12} \\ a_{21} & a_{22} \\ a_{31} & a_{32} \end{matrix} =$
.

$=$		$a_{11} \cdot a_{22} \cdot a_{33}$	$+ a_{12} \cdot a_{23} \cdot a_{31}$	$+ a_{13} \cdot a_{21} \cdot a_{32} -$
	$-$	$a_{13} \cdot a_{22} \cdot a_{31}$	$- a_{11} \cdot a_{23} \cdot a_{32}$	$- a_{12} \cdot a_{21} \cdot a_{33}$

.
Beispiel 2 - 27 mt9027 .
Die dreireihige Determinante von $A$ : .

$det A = |\begin{matrix} 1 & - 2 & 7 \\ 0 & 3 & 2 \\ 5 & - 1 & 4 \end{matrix}|$ .
.

.
.
.

PICT .

.
Beispiel 2 - 28 mt9015 .

$det A = |\begin{matrix} 4 & 2 & 1 \\ 10 & 5 & 0 \\ - 6 & - 3 & 1 \end{matrix}|$ =
.

.
.
.

PICT .

2.2.2 Laplace’scher Entwicklungssatz

Der Laplace’scher Entwicklungssatz ermöglicht die Berechnung der Determinante von Matrizen mit mehr als $3 * 3$ Elementen.
Streicht man bei einer Determinante $D$ die i-te Zeile und k-te Spalte, so heißt die verbliebene Determinante Unterdeterminante. Sie wird durch das Symbol $D_{i k}$ gekennzeichnet. Die mit dem Vorzeichenfaktor ${(- 1)}^{i + k}$ versehene Unterdeterminante $D_{i k}$ wird als algebraisches Komplement $A_{i k}$ bezeichnet.
$A_{i k} = {(- 1)}^{i + k} \cdot D_{i k}$

Man kann sich das Vorzeichen entsprechend einem Schachbrettmuster vorstellen:


$+$	$-$	$+$

$-$	$+$	$-$

$+$	$-$	$+$

Die Determinante von

A

läßt sich auch über die algebraischen Komplemente

A_{n k}

ermitteln:

$det A = |\begin{matrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{matrix}|$
.

$=$		$a_{11} \cdot a_{22} \cdot a_{33} + a_{12} \cdot a_{23} \cdot a_{31} + a_{13} \cdot a_{21} \cdot a_{32}$	$-$
	$-$	$a_{13} \cdot a_{22} \cdot a_{31} - a_{11} \cdot a_{23} \cdot a_{32} - a_{12} \cdot a_{21} \cdot a_{33}$	$=$

$=$	$a_{11} \cdot (\underset{︸}{a_{22} \cdot a_{33} - a_{23} \cdot a_{32}})$	$- a_{12} \cdot (\underset{︸}{a_{21} \cdot a_{33} - a_{23} \cdot a_{31}})$	$+ a_{13} \cdot (\underset{︸}{a_{21} \cdot a_{32} - a_{22} \cdot a_{31}})$
	$D_{11}$	$D_{12}$	$D_{13}$

$D_{11} = |\begin{matrix} ⋮ & . . . & . . . \\ ⋮ & a_{22} & a_{23} \\ ⋮ & a_{32} & a_{33} \end{matrix}| = |\begin{matrix} a_{22} & a_{23} \\ a_{32} & a_{33} \end{matrix}| = a_{22} \cdot a_{33} - a_{23} \cdot a_{32}$ .

$D_{12} = |\begin{matrix} . . & ⋮ & . . . \\ a_{21} & ⋮ & a_{23} \\ a_{31} & ⋮ & a_{33} \end{matrix}| = |\begin{matrix} a_{21} & a_{23} \\ a_{31} & a_{33} \end{matrix}|$ $= a_{21} \cdot a_{33} - a_{23} \cdot a_{31}$ .

$D_{13} = |\begin{matrix} . . & . . . & ⋮ \\ a_{21} & a_{22} & ⋮ \\ a_{31} & a_{32} & ⋮ \end{matrix}| = |\begin{matrix} a_{21} & a_{21} \\ a_{31} & a_{32} \end{matrix}|$ $= a_{21} \cdot a_{32} - a_{22} \cdot a_{31}$ .
.

Damit kann man die Determinante $D$ in der Form
$D = a_{11} D_{11} - a_{12} D_{12} + a_{13} D_{13}$ bzw.
$D = a_{11} A_{11} + a_{12} A_{12} + a_{13} D_{13} = \sum_{k = 1}^{3} a_{1 k} \cdot A_{1 k}$
schreiben.

Allgemein kann man nach dem Laplaceschen Entwicklungssatz die Determinante einer $3 x 3$ -Matrix durch Entwickeln nach einer Zeile oder Spalte berechnen:
$D = \sum_{k = 1}^{3} a_{i k} \cdot A_{i k}$ oder $D = \sum_{i = 1}^{3} a_{i k} \cdot A_{i k}$ .
Die $A_{i k}$ sind die algebraischen Komplemente von $a_{i k}$ in $D$ : $A_{i k} = {(- 1)}^{i + k} \cdot D_{i k}$ .

.
Beispiel 2 - 29 mt9016 .
$det A = |\begin{matrix} 1 & 4 & 6 \\ 5 & - 2 & 3 \\ 0 & 1 & 7 \end{matrix}|$ .
.
.

.
.

PICT .

2.2.3 Determinanten höherer Ordnung

Für (quadratische!) $n x n$ -Matrizen können Determinanten n-ter Ordnung entsprechend angegeben werden:

$D = det A = |\begin{matrix} a_{11} & a_{12} & … & a_{1 n} \\ a_{21} & a_{22} & … & a_{2 n} \\ ⋮ & ⋮ & ⋮ \\ a_{n 1} & a_{n 2} & … & a_{n n} \end{matrix}|$

.

Die o.a. Rechenregeln für Determinanten gelten entsprechend.

Die Determinante kann man nach dem Laplaceschen Entwicklungssatz einer $n x n$ -Matrix durch Entwickeln nach einer Zeile oder Spalte berechnen: .
.
$D = \sum_{k = 1}^{n} a_{i k} \cdot A_{i k}$ oder $D = \sum_{i = 1}^{n} a_{i k} \cdot A_{i k}$ . .
.
Die $A_{i k}$ sind die algebraischen Komplemente von $a_{i k}$ in $D$ : $A_{i k} = {(- 1)}^{i + k} \cdot D_{i k}$

Vorgehen bei der Bestimmung einer n-reihigen Determinante:

1.: Man versucht, mit Hilfe elementarer Umformungen zunächst die Elemente einer Zeile (oder Spalte) bis auf eines (oder wenigen) auf Null zu bringen.
2.: Durch Entwicklung nach diesen Elementen erhält man eine (n-1)-reihige Unterdeterminante.
3.: Dies wird solange wiederholt, bis man z.B. 3-reihige Determinanten nach der Regel von Sarrus bestimmen kann. .

.
Beispiel 2 - 30 mt9017 .

$det A = |\begin{matrix} 2 & 2 & 0 & 0 \\ 4 & 1 & - 3 & 2 \\ 0 & - 1 & 2 & 1 \\ 1 & - 1 & 0 & 0 \end{matrix}| =$ .
.

.
.

PICT .

.
Beispiel 2 - 31 mt9018 .
$det A = |\begin{matrix} - 1 & 1 & 0 & - 2 & 0 \\ 0 & 2 & 1 & - 1 & 4 \\ 1 & 0 & 0 & - 3 & 1 \\ 1 & 2 & 0 & 0 & 3 \\ 0 & - 2 & 1 & 2 & 2 \end{matrix}| =$
.

.
.
.

PICT .

2.2.4 Lösbarkeit von Gleichungssystemen

Bei der Lösbarkeit von Gleichungssystemen gibt es die drei Fälle:
Ein Gleichungssystem hat

$\}$

eine oder keine oder unendlich viele

Lösungen. .
.
Mit Hilfe des Rangs einer Matrix (s.u.) läßt sich eine Angabe über die Lösbarkeit machen:

PICT

Abbildung 4: Rang einer Matrix

.
.

Neben dem Rang $R g$ einer Matrix ist es hilfreich zu wissen, was eine

reguläre
singuläre
inverse
orthogonale

Matrix ist.

2.2.5 Reguläre Matrix

Eine n-reihige, quadratische Matrix $A$ heißt regulär, wenn ihre Determinante einen von Null verschiedenen Wert besitzt. Anderenfalls heißt sie singulär. .
Beispiel 2 - 32:
Die Matrix .
$A = (\begin{matrix} 1 & 0 & 2 \\ - 1 & 4 & 1 \\ - 2 & 1 & 2 \end{matrix})$
.

ist regulär, da ihre Determinante einen von Null verschiedenen Wert (21) besitzt.

Die Matrix .

$A = (\begin{matrix} - 4 & 2 \\ 6 & - 3 \end{matrix})$
.

ist singulär, da ihre Determinante den Wert Null besitzt.

2.2.6 Inverse Matrix

Wie bereits gezeigt, sind Matrixprodukte nicht kommutativ. Man kann jedoch auf beiden Seiten einer Gleichung eine Multiplikation mit der gleichen Matrix durchführen (Rechts- oder Links-Multiplikation).
Hat man speziell eine Matrixgleichung mit einer einreihigen, quadratischen Matrix $A$ $A X = E$ ( $E$ : Einheitsmatrix), so heißt $X$ die zu $A$ inverse Matrix und wird durch das Symbol $A^{- 1}$ dargestellt.

Nicht alle Matrizen sind invertierbar. .
Beispiel 2 - 33 mt9019 .
Die Matrix .
$A = (\begin{matrix} 1 & 1 \\ 2 & 2 \end{matrix})$ .
.
Die Matrix $A$ müßte erfüllen: $A \cdot A^{- 1} = E$
.
.
.

.

Eine quadratische Matrix hat (wenn überhaupt) genau eine Inverse.
Besitzt eine Matrix $A$ eine inverse MAtrix $A^{- 1}$ , so heißt $A$ invertierbar. Die (ebenso n-rehige) Matrix $A^{- 1}$ wird auch Umkehrmatrix, Kehrmatrix oder Inverse von $A$ bezeichnet.
Es gilt: $A \cdot A^{- 1} = A^{- 1} \cdot A = E$ , d.h. $A$ und $A^{- 1}$ sind kommutativ.

Berechnung der inversen Matrix unter Verwendung von Unterdeterminanten
Für eine reguläre n-reihige (quadratische) Matrix $A$ kann man mit Hilfe von Unterdeterminanten die Inverse $A^{- 1}$ wie folgt berechnen:

$A^{- 1} = \frac{1}{det A} \cdot (\begin{matrix} A_{11} & A_{21} & … & A_{n 1} \\ A_{12} & A_{22} & … & A_{n 2} \\ ⋮ & ⋮ & ⋮ \\ A_{1 n} & A_{2 n} & … & A_{n n} \end{matrix})$ .
.

$⨳¡$ Man beachte die Reihenfolge der Indizes !

$A_{k i} = A_{i k}^{T}$ $A_{i k}$ ist das algebraische Komplement, also die mit dem Vorzeichenfaktor ${(- 1)}^{i + k}$ versehene Unterdeterminante $D_{i k}$ : $A_{i k} = {(- 1)}^{i + k} \cdot D_{i k}$

Nachteil des Verfahrens ist der hohe Rechenaufwand bei größeren Matrizen.

Stattdessen wird eine Matrix häufig nach dem Gaußschen Algorithmus (Gauß-Jordan-Verfahren) invertiert. Hierbei bildet man aus einer Matrix $A$ und einer n-reihigen Einheitmatrix eine erweiterte Matrix

$(A | E) = (\underset{A}{\underset{︸}{\begin{matrix} a_{11} & a_{12} & … & a_{1 n} \\ a_{21} & a_{22} & … & a_{2 n} \\ ⋮ & ⋮ & ⋮ \\ a_{m 1} & a_{m 2} & … & a_{m n} \end{matrix}}} \underset{E}{\underset{︸}{\begin{matrix} 1 & 0 & … & 0 \\ 0 & 1 & … & 0 \\ ⋮ & ⋮ & ⋮ \\ 0 & 0 & … & 1 \end{matrix}}})$ .

Mit Hilfe elementarer Zeilenumformungen wird diese Matrix so umgeformt, daß auf der linken Seite die Einheitsmatrix steht. Auf der rechten Seite steht dann die Inverse:

$(\underset{E}{\underset{︸}{\begin{matrix} 1 & 0 & … & 0 \\ 0 & 1 & … & 0 \\ ⋮ & ⋮ & ⋮ \\ 0 & 0 & … & 1 \end{matrix}}} \underset{B = A^{- 1}}{\underset{︸}{\begin{matrix} b_{11} & b_{12} & … & b_{1 n} \\ b_{21} & b_{22} & … & b_{2 n} \\ ⋮ & ⋮ & ⋮ \\ b_{m 1} & b_{m 2} & … & b_{m n} \end{matrix}}}) = (E | A^{- 1})$ .
.
Beispiel 2 - 34 mt9028

$A = (\begin{matrix} 1 & 0 & - 1 \\ - 8 & 4 & 1 \\ - 2 & 1 & 0 \end{matrix})$ . .
.
$()$

=.
.
.
.

PICT .

2.2.7 Übungen

2.2.8 Orthogonale Matrix

Ensteht aus dem Produkt einer n-reihigen Matrix $A$ und ihrer Transponierten $A^{- 1}$ eine Einheitsmatrix
$A \cdot A^{T} = E$ ,
so heißt die Matrix $A$ orthogonal.
Es gilt: .
$det (A \cdot A^{T}) = det (A) \cdot \underset{det A}{\underset{︸}{(det (A^{T}))}} = {(det A)}^{2} = det E = 1$ . .
.
Damit ist
$det A = 1$ oder $det A = - 1$ .
Dann gilt auch:
$A \cdot A^{- 1} = A^{- 1} \cdot A = E$ .
Multipliziert man nun auf beiden Seiten von links mit der inversen Matrix $A^{- 1}$ , so erhält man:
$A^{- 1} \cdot (A \cdot A^{T}) = A^{- 1} \cdot E$ und weiter

$A^{- 1} \cdot (A \cdot A^{T}) = \underset{E}{\underset{︸}{(A^{- 1} \cdot A)}} \cdot A^{T} = E \cdot A^{T} = A^{T}$
$A^{- 1} \cdot E = A^{- 1}$
Damit ist $A^{T} = A^{- 1}$ .
.
Das heißt, eine Orthogonale Matrix geht bei der Transposition in ihre inverse über. Dann gilt auch:
$A \cdot A^{T} = A^{T} \cdot A = E$ .

Eigenschaften einer orthogonalen Matrix

1.: Die Zeilen- bzw. Spaltenvektoren einer orthogonalen Matrix $A$ bilden ein orthonormiertes System, stellen also zueinander orthogonale Einheitsvektoren dar (daher auch ihr Name)
2.: Die Determinante einer orthogonalen Matrix $A$ besitzt den Wert $+ 1$ oder $- 1$ :
$det A = \pm 1$
Eine orthogonale Matrix ist daher stets regulär (der Umkehrschluß darf daraus nicht gezogen werden).
3.: Bei einer orthogonalen Matrix $A$ sind die Transponierte $A^{T}$ und die Inverse $A^{- 1}$ identisch: .
$A^{T} = A^{- 1}$ .

Beispiel für eine orthogonale Matrix: .
Beispiel 2 - 35 mt9020 .
$A = (\begin{matrix} \frac{1}{2} \sqrt{2} & 0 & - \frac{1}{2} \sqrt{2} \\ \frac{1}{2} \sqrt{2} & 0 & \frac{1}{2} \sqrt{2} \\ 0 & 1 & 0 \end{matrix})$ .
Mit $A^{T} = A^{- 1}$ muss gelten: .
$A \cdot A^{T} = E$ .

.
.
.

PICT .

2.2.9 Rang einer Matrix

Zunächst wird der Begriff der Unterdeterminante auf nicht quadratische Matrizen ausgedehnt, indem man einfach eine oder mehrere Zeilen oder Spalten streicht, bis man eine quadratische pxp-Matrix erhält, von der dann die Unter-Determinante p-ter Ordnung gebildet werden kann.

Beispiel 2 - 36:

$A = (\begin{matrix} 2 & 1 & - 4 \\ 0 & 8 & 3 \end{matrix})$
.

hat die Unterdeterminanten

$|\begin{matrix} 1 & - 4 \\ 8 & 3 \end{matrix}| = 35$ , $|\begin{matrix} 2 & - 4 \\ 0 & 3 \end{matrix}| = 6$ und $|\begin{matrix} 2 & 1 \\ 0 & 8 \end{matrix}| = 16$ ,
.

aber auch sechs einreihige Unterdeterminanten:

$|3| = 3$ , $|8| = 8$ , $|0| = 0$ , $|- 4| = - 4$ , $|1| = 1$ , $|2| = 2$ .

Bildet man nun von einer Matrix alle möglichen Unterdeterminanten und betrachtet beginnend von der höchsten Ordnung deren Werte, so ergibt die Ordnung der ersten Determinante, die verschieden von Null ist, den Rang dieser Matrix.

$\Rightarrow$ Der Rang einer Matrix ist die höchste Ordnung aller von Null verschiedenen Unterdeterminanten von A.

Bestimmung des Rangs einer Matrix $A_{m n}$ :
Ist $m \leq n$ , vertauscht man einfach m und n.
Der Rang der Matrix ist höchstens n.

1.: man beginnt mit der höchsten Ordnung m
2.: man bildet die Unterdeterminanten der Ordnung m
3.: Ist eine dieser Unterdeterminanten verschieden von Null ?
Wenn ja, $\Rightarrow r g (A_{m n}) = m \Rightarrow$ Ende
4.: anderenfalls reduziert man $m$ um 1 und geht zu Schritt 2

.
Alternativ: .
Man formt die Matrix um in Richtung Dreiecksgestalt. Die Anzahl der Nicht-Nullzeilen gibt den Rang der Matrix an. .
.
Der Rang einer Matrix $A$ ändert sich bei den folgenden Umformungen nicht:

1.: Vertauschen zweier Zeilen (oder Spalten)
2.: Multiplikation oder Division einer Zeile oder Spalte mit einer beliebigen, von Null verschiedenen Zahl
3.: Addition eines Vielfachen einer anderen Zeile oder Spalte zu einer Zeile bzw. Spalte.

Beispiel 2 - 37 mt9021
Rang der Matrix .
$A_{23} = (\begin{matrix} 7 & 4 & 9 \\ 7 & 3 & 0 \end{matrix})$ .
.

.
.

PICT .

Beispiel 2 - 38 mt9022
Rang der Matrix .

$A = (\begin{matrix} 1 & 1 & 1 & 0 \\ 2 & - 1 & 1 & 3 \\ 1 & - 2 & 0 & 3 \end{matrix})$

.

.
.

PICT .

Man kann zeigen: .
Für jede Matrix $A$ ist die maximale Anzahl unabhängiger Zeilenvektoren gleich der Anzahl unabhängiger Spaltenvektoren. Diese maximale Anzahl heißt Rang einer Matrix $r g (A)$ .

2.2.10 Anwendungen auf Lineare Gleichungssysteme

Wie bereits gezeigt, kann das lineare Gleichungssystem geschrieben werden als $A \cdot \vec{x} = \vec{c}$ mit den Koeffizienten $a_{i k}$ und den Absolutgliedern (Konstanten): $c_{i}$ .
$A \cdot \vec{x} = \vec{c} \Rightarrow$

$a_{11} \cdot x_{1}$	$+ a_{12} \cdot x_{2}$	$+ a_{13} \cdot x_{3}$	$\dots$	$+ a_{1 n} \cdot x_{n}$	$=$	$c_{1}$
$a_{21} \cdot x_{1}$	$+ a_{22} \cdot x_{2}$	$+ a_{23} \cdot x_{3}$	$\dots$	$+ a_{2 n} \cdot x_{n}$	$=$	$c_{2}$
$a_{31} \cdot x_{1}$	$+ a_{32} \cdot x_{2}$	$+ a_{33} \cdot x_{3}$	$\dots$	$+ a_{3 n} \cdot x_{n}$	$=$	$c_{3}$
$⋮$	$⋮$	$⋮$	$⋮$ $⋮$ $⋮$	$⋮$		$⋮$

$\Rightarrow$	$A \cdot \vec{x}$	$=$	$\vec{c}$	mit $\vec{x} = (\begin{matrix} x_{1} \\ x_{2} \\ x_{3} \\ ⋮ \end{matrix})$	und $\vec{c} = (\begin{matrix} c_{1} \\ c_{2} \\ c_{3} \\ ⋮ \end{matrix})$

.
.
Das lineare Gleichungssystem heißt homogen, wenn

\vec{c} =

ist, d.h. wenn alle Absolutglieder verschwinden:

A \cdot \vec{x} = \vec{0}

.
Ist mindestens ein Absolutglied von Null verschieden, so ist das Gleichungssystem inhomogen. .
Für

n = m

hat man ein quadratisches Gleichungssystem vor sich.

2.2.11 Lösungsverhalten eines linearen (m,n)-Gleichungssystems

Das Lösungsverhalten eines linearen (m,n)-Gleichungssystems wird durch die Homogenität/Inhomogenität des Gleichungssystems entscheidend geprägt:

1.: Inhomogenes lineares Gleichungssystem $A \cdot \vec{x} = \vec{c}$
Das System besitzt entweder genau eine Lösung oder unendlich viele Lösungen oder überhaupt keine Lösung.
2.: Homogenes lineares Gleichungssystem $A \cdot \vec{x} = \vec{0}$
Das System besitzt entweder genau eine Lösung, nämlich die triviale Lösung $\vec{x} = 0$ , oder unendlich viele Lösungen (darunter die triviale Lösung).

Ein gegebenes Gleichungssystem

$a_{11} \cdot x_{1}$	$+ a_{12} \cdot x_{2}$	$+ a_{13} \cdot x_{3}$	$\dots$	$+ a_{1 n} \cdot x_{n}$	$=$	$c_{1}$
$a_{21} \cdot x_{1}$	$+ a_{22} \cdot x_{2}$	$+ a_{23} \cdot x_{3}$	$\dots$	$+ a_{2 n} \cdot x_{n}$	$=$	$c_{2}$
$a_{31} \cdot x_{1}$	$+ a_{32} \cdot x_{2}$	$+ a_{33} \cdot x_{3}$	$\dots$	$+ a_{3 n} \cdot x_{n}$	$=$	$c_{3}$
$⋮$	$⋮$	$⋮$	$⋮$ $⋮$ $⋮$	$⋮$		$⋮$

kann man durch äquivalente Umformungen in ein gestaffeltes Gleichungssystem der Form

$a_{11}^{*} \cdot x_{1}$	$+ a_{12}^{*} \cdot x_{2}$	$+ \dots$	$+ a_{1 r}^{*} \cdot x_{r}$	$\dots$	$+ a_{1 n}^{*} \cdot x_{n}$	$=$	$c_{1}^{*}$
	$+ a_{22}^{*} \cdot x_{2}$	$+ \dots$	$+ a_{2 r}^{*} \cdot x_{r}$	$\dots$	$+ a_{2 n}^{*} \cdot x_{n}$	$=$	$c_{2}^{*}$
		$⋮$	$⋮$		$⋮$		$⋮$
			$+ a_{r r}^{*} \cdot x_{r}$	$\dots$	$+ a_{r n}^{*} \cdot x_{n}$	$=$	$c_{r}^{*}$
					$0$	$=$	$c_{r + 1}^{*}$
					$0$	$=$	$c_{r + 2}^{*}$
					$⋮$		$⋮$
					$0$	$=$	$c_{m}^{*}$

überführen.

Abbildung 5: eine / unendlich viele / keine Lösungen

.
In Matrixschreibweise :
$A \cdot \vec{x} = \vec{c}$ wird durch äquivalente Umformungen in $A^{*} \cdot \vec{x^{*}} = \vec{c^{*}}$ überführt.
$\binom{A}{(A | \vec{c})}\} \to_{Z e i l e n u m f o r m u n g e n}^{e l e m e n t a r e} \{\binom{A^{*}}{(A^{*} | \vec{c^{*}})}$

.

Damit das Gleichungssystem lösbar ist, muss die erweiterte Koeffizientenmatrix $(A^{*} | \vec{c^{*}})$ die spezielle Form

$(A^{*} | \vec{c^{*}}) = (\underset{A^{*}}{\underset{︸}{\begin{matrix} a_{11}^{*} & ^{*} a_{12} & … & a_{1 r}^{*} & … & a_{1 n}^{*} \\ 0 & ^{*} a_{22} & … & a_{2 r}^{*} & … & a_{2 n}^{*} \\ ⋮ & ⋮ & ⋮ \\ 0 & 0 & … & a_{r r}^{*} & … & a_{r n}^{*} \\ 0 & 0 & … & 0 & … & 0 \\ ⋮ & ⋮ & ⋮ \\ 0 & 0 & … & 0 & … & 0 \end{matrix}}} \underset{\vec{c^{*}}}{\underset{︸}{\begin{matrix} c_{1}^{*} \\ c_{2}^{*} \\ ⋮ \\ 0 \\ 0 \\ ⋮ \\ 0 \end{matrix}}})$ .
.
annehmen.
Sowohl die Matrizen $a^{*}$ als auch $(A^{*} | \vec{c^{*}})$ sind von trapezförmiger Gestalt und enthalten in den letzten (m-r) Zeilen nur Nullen. Sie stimmen daher mit ihrem Rang überein:

$R g (A^{*}) = R g (A^{*} | c^{*}) = r$ .

Da die erweiterten Matrizen $(A | c)$ und $(A^{*} | c^{*})$ durch äquivalente Umformungen / elementare Zeilenumformungen ineinander übergegangen sind, sind die korrespondierenden Matrizen ebenso ranggleich.

Dann gilt jedoch:

Ein lineares (m,n)-System $A \cdot \vec{c} = \vec{c}$ ist nur dann lösbar, wenn der Rang der Koeffizientenmatric $A$ mit dem Rang der erweiterten Koeffizientenmatrix $(A | c)$ übereinstimmt:

$R g (A) = R g (A | c) = r$ ( $r \leq m; r \leq n)$

Fallunterscheidungen

1.

Fall:

r = n

Das gestaffelte System

A^{\cdot} \vec{x} = \vec{c^{*}}

besitzt für r =n die quadratische Form:

$a_{11}^{*} \cdot x_{1}$	$+ a_{12}^{*} \cdot x_{2}$	$+ \dots$	$+ a_{1 n}^{*} \cdot x_{n}$	$=$	$c_{1}^{*}$
	$+ a_{22}^{*} \cdot x_{2}$	$+ \dots$	$+ a_{2 n}^{*} \cdot x_{n}$	$=$	$c_{2}^{*}$
			⋮		⋮
			$a_{n n}^{*} \cdot x_{n}$	$=$	$c_{n}^{*}$

In Matrixschreibweise :

$(A^{*} | \vec{c^{*}}) = (\underset{A^{*}}{\underset{︸}{\begin{matrix} a_{11}^{*} & ^{*} a_{12} & … & a_{1 n}^{*} \\ 0 & ^{*} a_{22} & … & a_{2 n}^{*} \\ ⋮ & ⋮ & ⋮ \\ 0 & 0 & … & a_{n n}^{*} \end{matrix}}} \underset{\vec{c_{n}^{*}}}{\underset{︸}{\begin{matrix} c_{1}^{*} \\ c_{2}^{*} \\ ⋮ \\ c_{n}^{*} \end{matrix}}})$
.
.

Nun kann man durch Rückwärtseinsetzen die Werte für $\vec{x}$ bestimmen. Das Gleichungssystem besitzt genau eine Lösung

2.

Fall:

r < n

Das gestaffelte System

A^{*} \cdot \vec{x} = \vec{c^{*}}

hat rechteckige Gestalt für

r < n

$a_{11}^{*} \cdot x_{1}$	$+ a_{12}^{*} \cdot x_{2}$	$+ \dots$	$+ a_{1 r}^{*} \cdot x_{r}$	$\dots$	$+ a_{1 n}^{*} \cdot x_{n}$	$=$	$c_{1}^{*}$
	$+ a_{22}^{*} \cdot x_{2}$	$+ \dots$	$+ a_{2 r}^{*} \cdot x_{r}$	$\dots$	$+ a_{2 n}^{*} \cdot x_{n}$	$=$	$c_{2}^{*}$
			$⋮$	⋮			⋮
			$a_{r r}^{*} \cdot x_{r}$	$\dots$	$+ a_{r n}^{*} \cdot x_{n}$	$=$	$c_{r}^{*}$

Damit haben wir mehr Unbekannte als Gleichungen:

n > r

. Davon sind

n - r

der Unbekannten, z.B.

x_{r + 1}, x_{r + 2}, \dots, x_{n}

frei wählbare Größen (Parameter).
Durch Rückwärtseinsetzen erhält man die unendlich vielen Lösungen des gestaffelten Systems, die dann durch die Parameter ausgedrückt werden.

Zusammenfassung: Ein Lineares Gleichungssystem ist nur lösbar, wenn Koeffzientematrix $A$ und erweiterte Matrix $(A | c)$ ranggleich sind:

$R g (A) = R g (A | c) = r$

Im Falle der Lösbarkeit besitzt das lineare Gleichungssystem die folgende Lösungsmenge:
Für $r = n$ : Genau eine Lösung
Für $r < n$ : Unendlich viele Lösungen

In einem homogenen System $A \cdot \vec{x} = \vec{0}$ ist die Lösbarkeitsbedingung $R g (A) = R g (A | c)$ stets erfüllt.

Abbildung 6: Lösbarkeit von Gleichungssystemen

Beispiel 2 - 39 mt9023
Das Gleichungssystem

$3 x_{1}$	$-$	$4 x_{2}$	$=$	$2$
$- x_{1}$	$+$	$5 x_{2}$	$=$	$4$
$5 x_{1}$	$+$	$2 x_{2}$	$=$	$12$

.
.

PICT .

.
Beispiel 2 - 40 mt9024 .
Das Gleichungssystem

$4 x_{1}$	$-$	$x_{2}$	$-$	$x_{3}$	$=$	$6$
$x_{1}$			$+$	$2 x_{3}$	$=$	$0$
$- x_{1}$	$+$	$2 x_{2}$	$+$	$2 x_{3}$	$=$	$2$
$3 x_{1}$	$-$	$x_{2}$			$=$	$3$

hat genau eine Lösung: .
.
.

PICT .

.
Beispiel 2 - 41 mt9029 .
Das Gleichungssystem

$x_{1}$	$+$	$x_{2}$	$+$	$x_{3}$	$+$	$3 x_{4}$	$=$	$0$
		$2 x_{2}$			$+$	$2 x_{4}$	$=$	$5$
$- x_{1}$	$-$	$x_{2}$	$-$	$2 x_{3}$	$-$	$2 x_{4}$	$=$	$4$
$2 x_{1}$	$+$	$4 x_{2}$	$+$	$2 x_{3}$	$+$	$8 x_{4}$	$=$	$5$

.
ist lösbar und hat unendlich viele Lösungen: .
.
.

PICT .

2.2.12 Übungen

2.2.13 Lösung linearer Gleichungssysteme mit der Cramer’schen Regel

Ein lineares (n,n)-Gleichungssystem $A \cdot \vec{x} = \vec{c}$ besitzt genau eine Lösung, wenn die Koeffizientenmatrix $A$ regulär ist. Dann existiert auch die zu $A$ inverse Matrix $A^{- 1}$ , und die Lösung läßt sich wie folgt berechnen:
Man multipliziert die Matrizengleichung $A \cdot \vec{x} = \vec{c}$ von links mit $A^{- 1}$ :
$A^{- 1} \cdot A \cdot \vec{x} = A^{- 1} \cdot \vec{c}$

$A^{- 1} \cdot \vec{c} = A^{- 1} \cdot A \cdot \vec{x} = \underset{︸}{(A^{- 1} \cdot A)} E \cdot \vec{x} = E \cdot \vec{x} = \vec{x}$

Damit wird der Lösungsvektor

$\vec{x} = A^{- 1} \cdot \vec{c} = \frac{1}{det A} \cdot (\begin{matrix} A_{11} & A_{21} & … & A_{n 1} \\ A_{12} & A_{22} & … & a_{n 2} \\ ⋮ & ⋮ & ⋮ \\ A_{1 n} & A_{2 n} & … & A_{n n} \end{matrix}) \cdot (\begin{matrix} c_{1} \\ c_{2} \\ ⋮ \\ c_{n} \end{matrix})$

$= \frac{1}{det A} \cdot (\begin{matrix} c_{1} \cdot A_{11} & + c_{2} \cdot A_{21} & + … & + c_{n} \cdot A_{n 1} \\ c_{1} \cdot A_{12} & + c_{2} \cdot A_{22} & + … & + c_{n} \cdot A_{n 2} \\ ⋮ & ⋮ & ⋮ \\ c_{1} \cdot A_{1 n} & + c_{2} \cdot A_{2 n} & + … & + c_{n} \cdot A_{n n} \end{matrix})$ ,
.

oder in komponentenweiser Darstellung:

$x_{1} = \frac{c_{1} A_{11} + c_{2} A_{21} + \dots + c_{n} A_{n 1}}{det A}$
$x_{2} = \frac{c_{1} A_{12} + c_{2} A_{22} + \dots + c_{n} A_{n 2}}{det A}$
⋮ ⋮
$x_{n} = \frac{c_{1} A_{1 n} + c_{2} A_{2 n} + \dots + c_{n} A_{n n}}{det A}$
.

Den Zähler kann man auch schreiben als Determinante:

$D_{1} = |\begin{matrix} c_{1} & a_{12} & a_{13} & … & a_{1 n} \\ c_{2} & a_{22} & a_{23} & … & a_{2 n} \\ ⋮ & ⋮ & ⋮ \\ c_{n} & a_{n 2} & a_{n 3} & … & a_{n n} \end{matrix}|$ ,
.

was sich sofort verifizieren läßt, indem man einfach diese Determinante nach den Elementen der ersten Spalte entwickelt.
Mit der Vereinbarung $D = det A$ kann man dann vereinfacht schreiben:
$x_{1} = \frac{D_{1}}{D}, x_{2} = \frac{D_{2}}{D}, x_{3} = \frac{D_{3}}{D}$ bzw. $x_{i} = \frac{D_{i}}{D}$ ,
was als Cramer’sche Regel bekannt ist.

Die Cramer’sche Regel scheint zwar einfach anwendbar, ist aber in der Regel ineffizient, insbesondere bei größeren Zahlen von m und n. .
Beispiel 2 - 42 mt9030
Das Gleichungssystem

$2 x_{1}$	$+$	$x_{2}$	$+$	$3 x_{3}$	$=$	$8$
$- x_{1}$	$-$	$4 x_{2}$	$+$	$x_{3}$	$=$	$3$
$x_{1}$	$+$	$2 x_{2}$	$-$	$4 x_{3}$	$=$	$1$

.
hat genau eine Lösung, da die Koeffizientendeterminante .

det A = |\begin{matrix} 2 & 1 & 3 \\ - 1 & - 4 & 1 \\ 1 & 2 & - 4 \end{matrix}| = 32 + 1 - 6 + 12 - 4 - 4 = 31 \neq 0

ist. .
.

Anwendung der Cramer’schen Regel: .
.
.

PICT .

2.2.14 Auswirkungen von Rundungsfehlern

Die bisher aufgeführten Verfahren

Gaußsches Verfahren
Gauß-Jordan-Verfahren
Cramer’sche Regel

bergen die Gefahr von Rundungsfehlern.
Beispiel 2 - 43:
Das Gleichungssystem

$\begin{matrix} x_{1} & + & x_{2} & = & 2 \\ x_{1} & + & 1, 0001 \cdot x_{2} & = & 2, 0001 \end{matrix}$

hat $(1, 1)$ als Lösung. Lag nun beispielsweise ein Rundungsfehler vor,

$\begin{matrix} x_{1} & + & x_{2} & = & 2 \\ x_{1} & + & 1, 0001 \cdot x_{2} & = & 2 \end{matrix}$ ,

erhält man als Lösung $(2, 0)$ , was deutlich von der ersten Lösung abweicht.
Sind die Rundungseffekte noch stärker,so erhält man

$\begin{matrix} x_{1} & + & x_{2} & = & 2 \\ x_{1} & + & x_{2} & = & 2 \end{matrix}$ ,

mit unendlich vielen Lösungen $(2 - λ, λ), λ \in R$ , was nochmals deutlich von der ersten Lösung abweicht.

Wenn sehr kleine Veränderungen der Werte solch große Auswirkungen auf die Lösungen haben, spricht man von einem schlecht konditioniertem Gleichungssystem.
Bem Gleichungssystem
$\begin{matrix} 0, 00001 \cdot x_{1} & + & x_{2} & = & 1 \\ x_{1} & + & x_{2} & = & 2 \end{matrix}$

tritt dies beispielsweise nicht auf, das Gleichungssystem ist gut konditioniert. Ein Runden ergibt
$\begin{matrix} x_{2} & = & 1 \\ x_{1} & + & x_{2} & = & 2 \end{matrix}$ ,

und man erhält als Lösung $(1, 1)$ . Bei Anwendung des Gauß-Verfahrens erhält man jedoch
$\begin{matrix} 0, 00001 \cdot x_{1} & + & x_{2} & = & 1 \\ - 9999 \cdot x_{2} & = & - 99998 \end{matrix}$

und daraus $x_{2} = 0, 99990$ . Rundet man diesen Wert auf 1, so ergibt sich aus der ersten Gleichung
$0, 0001 \cdot x_{1} + 1 = 1 \Rightarrow x_{1} = 0$ ,

also eine Lösung $(0, 1)$ und nicht $(1, 1)$ wie erwartet. Der Fehler ließe sich durch entsprechende Umstellung vermeiden, indem man z.B. die Variablen vertauscht:

$\begin{matrix} x_{2} & + & 0, 00001 \cdot x_{1} = & 1 \\ x_{2} & + & 1 \cdot x_{1} & = & 2 \end{matrix}$

was zu den Gleichungen führt:

$\begin{matrix} x_{2} & + & 0, 00001 \cdot x_{1} = & 1 \\ 0, 9999 \cdot x_{1} & = & 1 \end{matrix}$

und daraus nach Rundung das Ergebnis $(1, 1)$ . Indem man die Diagonalelemente durch Umstellung möglichst groß macht (Pivotisieren), läßt sich dieser Effekt meist reduzieren.

3 Anwendungen

3.1 Anwendungen in der Ökologie, Eigenwerte und Eigenvektoren

3.1.1 Markov-Ketten und Übergangsmatrizen

Beispiel 3 - 44: Sie wohnen auf einer recht einsamen Insel. Auf dieser Insel gibt es nur einen Getränkeanbieter mit zwei Getränkesorten $T$ und $K$ . Der Anbieter hat festgestellt, daß pro Jahr 15 % der $T$ -Konsumenten zu $K$ und 4 % von $K$ zu $T$ wechseln. .
Das Konsumentenverhalten kann man graphisch so darstellen: .

Abbildung 7: Wechselverhalten der Getränkekonsumenten

.
Bezeichnet man den Absatz des Getränks $K$ bzw. $T$ in diesem Jahr mit $k_{i}$ und im Folgejahr mit $k_{i + 1}$ bzw. $t_{i}$ und $t_{i + 1}$ , kann man die Gleichungen aufstellen: .
$\begin{matrix} k_{i + 1} & = & 0.85 \cdot k_{i} & + & 0.04 \cdot t_{i} \\ t_{i + 1} & = & 0.15 \cdot k_{i} & + & 0.96 \cdot t_{i} \end{matrix}$ .
.
Geht man über zur Matrixschreibweise, ergibt sich der Getränke-(Spalten-)vektor im Folgejahr als Produkt der Übergangsmatrix $M$ mit dem Getränke-(Spalten-)vektor des Vorjahres: .
.
#G
i+1 = ki+1 ti+1 = 0.850.04 0.15 0.96 ⋅ki ti .
.
.

#
Gi+1 = M⋅ #
Gi . .

Für einen Anfangs-Absatz von .

#
G0 = k0 k0 = 2000 3000 .
.
Fässern erhält man im Folgejahr einen Verkauf von .
#G
1 = k1 t1 = 0.850.04 0.15 0.96 ⋅2000 3000 = 1820 3180 .
.
Fässern. .
.
Im Folgejahr (gleiches Wechselverhalten vorausgesetzt) ergibt sich .
.
ein Verkauf von .
.
#
G2 = k2 t2 = 0.850.04 0.15 0.96 ⋅1820 3180 = 1674 3326 .
.
Fässern. .
.

Interpretiert man den jährlichen Verkauf von Getränkefässern als Beobachtung und die Wechselraten als (feste) ’Wahrscheinlichkeiten’, so können wir bei bekannten Verkaufszahlen eines Jahres auf die Verkaufszahlen im Folgejahr schließen. .
Derartige Prognosemodelle, die mit der Verkettung von Wahrscheinlichkeiten operieren, nennt man Markoff’sche Ketten : Jede Beobachtung ist nur von einer oder von einer beschränkten Anzahl vorhergehender Beobachtungen abhängig. .

3.1.2 Leslie-Diagramme und Leslie-Matrizen

In Analogie zu obigem Getränkebeispiel soll die Populationsentwicklung einer Schwalbenherde betrachtet werden. Bekannt seien die (jährliche) Existenzwahrscheinlichkeit von Küken (K) $L_{11} = 0.75$ (im Folgejahr sind nur noch drei Viertel übrig) sowie Erwachsener (E) von $L_{22} = 0.6$ . Jährlich wird die Hälfte der Küken erwachsen ( $L_{21} = 0.5$ ), und jährlich gebären die erwachsenen Schwalben 1.3-fachen Nachwuchs ( $L_{12} = 1.3$ ). .
Im Leslie-Diagramm werden die Übergangswahrscheinlichkeiten an den Pfeilen eingetragen. Ist eine Übergangswahrscheinlichkeit Null, so kann der Pfeil weggelassen werden. .

Abbildung 8: Leslie-Diagramm

Nun seien in einem Bestand 30 Erwachsene und 60 Küken. Wie groß ist der Bestand nach einem bzw. 2 Jahren ? .
Derartige Übergangsmatrizen (sie sind analog zu oben) werden in der theoretischen Ökologie zur Beschreibung von Populationen genutzt und wurden von P. H. Leslie formuliert. Hat man Daten über $n$ Altersklassen, dann ist die Leslie-Matrix vomn Typ $n$ x $n$ . .
In unserem Beispiel lautet sie: .

$L = (\begin{matrix} L_{11} & L_{12} \\ L_{21} & L_{22} \end{matrix}) = (\begin{matrix} 0.75 & 1.3 \\ 0.5 & 0.6 \end{matrix})$ . .
.

#
Si+1 = ki+1 ei+1 = L⋅ #
Si .
#Si+1 = 0.751.3 0.5 0.6 ⋅ki e i = 0.751.3 0.5 0.6 ⋅60 30 = 84 48 . .

Für das Folgejahr ist die Population: .
.

#
Si+2 = ki+2 ei+2 = L⋅L⋅ #
Si = 125.4 70.8 ≈125 71 .
.

3.1.3 Eigenwerte und Eigenvektoren

Gegeben sei folgende Leslie-Matrix: .
.
$L = (\begin{matrix} 1.5 & 2 \\ 0.08 & 0 \end{matrix})$ . .
.
Für einen Populationsvektor .
#S
i = 10 10 .
ergibt sich im Folgejahr .

#
Si+1 = 250.8 .
.
Für einen anderen Populationsvektor .

#
Si = 20 1 .
.
ergibt sich im Folgejahr .

.
#
Si+1 = 321.6 = 1.6⋅20 1 .
.
Das heißt, der Populationsvektor kann aus dem ursprünglichen Vektor durch Multiplikation .
mit 1.6 erzeugt werden. Wenn das Produkt einer Matrix $L$ mit einem Vektor #
s das Gleiche ergibt wie die Multiplikation des Vektors mit einer Zahl $λ$ , nennen wir diesen Vektor Eigenvektor . Die Zahl $λ$ bezeichnet man als Eigenwert . .
Wie findet man die Eigenwerte und Eigenvektoren ? .
Wir gehen von folgendem Ansatz aus: $L \cdot$ # s = λ⋅ .
Ergänzt um die Einheitsmatrix $I$ .
$L \cdot$ #
s = λ⋅I⋅ #
s .
$L \cdot$ -λ⋅I⋅ = 0.
$(L - λ \cdot I) \cdot$ = 0.
Diese Gleichung ist für von Null verschiedene Vektoren dann erfüllt, wenn .

$det L - λ \cdot I = 0$

$det (L - λ \cdot I) = det (\begin{matrix} 1.5 - λ & 2 \\ 0.08 & 0 - λ \end{matrix}) = (1.5 - λ) \cdot (- λ) - 0.08 \cdot 2 = λ^{2} - 1.5 \cdot λ - 0.16 = 0$ . .
.
Lösungen sind $λ_{1} = 1.6$ und $λ_{2} = - 0.1$ . .
Die Eigenvektoren erhält man nun, indem man das Gleichungssystem .
$L \cdot$ = λ⋅ jeweils für die Werte von $λ_{1}$ und $λ_{2}$ löst. .
Für $λ_{1} = 1.6$ ergibt sich: .
= 20 1 .
.
.

Für $λ_{2} = - 0.1$ erhält man unendlich viele Lösungen: $0.8 \cdot s_{1} = s_{2}$ .
Sind nun die Populationsgrößen Eigenvektoren der Leslie-Matrizen, so kann man die Folgepopulationen einfach durch (ggf. mehrfache) Multiplikation des Eigenwerts mit dem Vektor bestimmen: .
#
si+n = λn⋅ #
si . .

3.2 Mischungen

3.2.1 Bestimmung von Zutatenmengen

Stellt man ein Gemisch her aus .
der Menge $x_{1}$ von der Komponente $A_{1}$ , .
der Menge $x_{2}$ von der Komponente $A_{2}$ , .
.............. .
der Menge $x_{k}$ von der Komponente $A_{k}$ , .
spricht man von einem Mischungsverhältnis $x_{1} : x_{1} : x_{2} : . . . . : x_{k}$ wenn man zuvor erst alle Zahlen $x_{1}, x_{1}, x_{2}, . . . ., x_{k}$ mit einem gemeinsamen Faktor multipliziert, sodaß sie alle ganzzahlig werden, und anschließend alle durch ihren größten gemeinsamen Teiler dividiert. .
Beispiel 3 - 45: Eine Lösung habe die Komponenten A, B und C in den Mengen 15 ml, 30 ml und 45 ml. In ganzen Zahlen (multipliziert mit 100/ml): 15, 30 und 45. Dividiert durch den ggT 15 ergibt ein Mischungsverhältnis $1 : 2 : 3$ . .
.
Hat man nun verschiedene Lösungen bzw. Pulver mit verschiedenen Konzentrationen der Wirkstoffe, so stellt man zunächst die Summengleichung und danach die Bilanzgleichung je Wirkstoff auf. .
Beispiel 3 - 46: Gegeben seien drei Standardlösungen mit den Konzentrationen der Wirkstoffe A und B. Herauskommen soll eine Lösung der Menge L, bei denen die Konzentrationen vorgegeben sind: .
.


mol/l	$L_{1}$	$L_{2}$	$L_{3}$	L .

A	$A_{1}$	$A_{2}$	$A_{3}$	A .
B	$B_{1}$	$B_{2}$	$B_{3}$	B .

.
.
.
Mit diesen Vorgaben erhält man drei Gleichungen: .
.

Gesamtmengengleichung:	$x_{1} +$	$x_{2} +$	$x_{3} =$	$L$ .

Bilanzgleichung für A:	$A_{1} \cdot x_{1} +$	$A_{2} \cdot x_{2} +$	$A_{3} \cdot x_{3} =$	$A \cdot L$ .
Bilanzgleichung für B:	$B_{1} \cdot x_{1} +$	$B_{2} \cdot x_{2} +$	$B_{3} \cdot x_{3} =$	$B \cdot L$ .

.
.

Dieses Gleichungssystem kann man z.B. mit dem Gauß-Verfahren lösen. .
(Ein zuzugegebendes Lösungsmittel hat die Konzentrationen Null.) .
Beispiel 3 - 47 gs9050
Gegeben sind vier Lösungen:
Die Lösung $L_{1}$ mit einem Wirkstoffgehalt A von $6 g ∕ l$ , einem Wirkstoffgehalt B von $7 g ∕ l$ und einem Wirkstoffgehalt C von $0, 3 g ∕ l$ ,
die Lösung $L_{2}$ mit einem Wirkstoffgehalt A von $7 g ∕ l$ , einem Wirkstoffgehalt B von $8 g ∕ l$ und einem Wirkstoffgehalt V von $0, 5 g ∕ l$ ,
die Lösung $L_{3}$ mit einem Wirkstoffgehalt A von $8 g ∕ l$ , einem Wirkstoffgehalt B von $9 g ∕ l$ und einem Wirkstoffgehalt C von $0, 6 g ∕ l$ und
die Lösung Wein $L_{4}$ mit einem Wirkstoffgehalt A von $8 g ∕ l$ , einem Wirkstoffgehalt B von $10, 4 g ∕ l$ und einem Wirkstoffgehalt C von $0, 78 g ∕ l$ ,

Welche Mengen der vier Lösungen muss man einer Mischung zugeben, damit man $700 m l$ mit einem Wirkstoffgehalt A von $7, 5 g ∕ l$ , Wirkstoffgehalt B von $9 g ∕ l$ und einem Wirkstoffgehalt C von $0, 6 g ∕ l$ erhält ? .
.

PICT .

.
.
Bei der Aufstellung solcher Ansätze ist zu beachten, daß man bei $n$ Wirkstofffen $n + 1$ Lösungen (Bilanzgleichunge) benötigt. Es können hierbei Gleichungssysteme entstehen, die nicht lösbar oder unsinnig (z.B. negative Mengen) sind.

3.3 Produktionsprozesse

3.3.1 Matrizen zur Beschreibung von Produktionsprozessen

Nehmen wir an, daß in einer Fabrik n verschiedene Rohstoffe $r$ $r_{1}, r_{2}, . . ., r_{n}$ eingesetzt werden. Aus diesen Rohstoffen enstehen k Zwischenprodukte $e$ $e_{1}, e_{2}, e_{3}, . . . ., e_{n}$ . .
Dann kann die Herstellung in Matrixdarstellung beschrieben werden als .
$\vec{r} = A \cdot \vec{e}$ . .
Kennt man nun den Bedarf der einzelnen Endprodukte, so kann man über diese Gleichung den Rohstoffbedarf ermitteln. Kenn man umgekehrt den Rohstoffbestand, so kann man mittels der Inversen $A^{- 1}$ den Endproduktbestand bestimmen: .
$\vec{e} = A^{- 1} \cdot \vec{r}$ . .
Sind mehrere Fertigungsstrassen im Werk, so entspricht dies einfach einer Multiplikation der Produktionsmatrizen. .
.
Beispiel 3 - 48 gs0710 .
In einem Chemiebtrieb werden vier Rohstoffe $r_{1}$ , $r_{2}$ , $r_{3}$ und $r_{4}$ zu drei Zwischenprodukten $z_{1}$ , $z_{2}$ und $z_{3}$ verarbeitet. Aus diesen Zwischenprodukten entstehen in einem weiteren Prozess die drei Endprodukte $p_{1}$ , $p_{2}$ und $p_{3}$ .
Die Mengenverbräuche sind gegeben durch die Gleichungen

$r_{1}$	=	$z_{1}$			+	$z_{3}$
$r_{2}$	=	$2 z_{1}$	+	$z_{2}$	+	$z_{3}$
$r_{3}$	=		+	$z_{2}$	+	$z_{3}$
$r_{4}$	=	$z_{1}$	+	$z_{2}$	+	$2 z_{3}$

und

$z_{1}$	=	$p_{1}$	+	$2 p_{2}$	+	$p_{3}$
$z_{2}$	=	$2 p_{1}$	+	$3 p_{2}$	+	$p_{3}$
$z_{3}$	=	$4 p_{1}$	+	$2 p_{2}$	+	$2 p_{3}$

. .
Gesucht ist der Rohstoffbedarf, wenn 100 Einheiten von

p_{1}

, 80 Einheiten von

p_{2}

und 60 Einheiten von

p_{3}

hergestellt werden sollen.
.

.
.

PICT .

3.3.2 Übungen

3.4 lineare Un-Gleichungssysteme

3.4.1 Lineare Optimierung

Unter dem Begriff Lineare Optimierung (oder auch Linearer Programmierung) versteht man die Maximierung (Minimierung) einer linearen Funktion unter Nebenbedingungen in Ungleichheitsform.
Beispiel (s. Sydsaeter, Mathematik für Wirtschaftswissenschaftler) :
Ein Bäcker hat 150 kg Mehl, 22 kg Zucker und 27,5 kg Butter zur Verfügung, um zwei Arten von Kuchen zu backen. Nehmen Sie an, daß für die Produktion eines Dutzends Kuchen der Sorte A bzw. B folgende Zutaten benötigt werden: .


Sorte	Mehl	Zucker	Butter

A	3	1.0	1
B	6	0.5	1

.
Die Erlöse: Ein Dutzend verkaufter Kuchen A ergibt 20 , ein Dutzend verkaufter Kuchen B ergibt 30 .
Wieviele Dutzend Kuchen der Sorten A (entspricht

x_{1}

) und B (entspricht

x_{2}

) maximieren nun den Erlös ?
Die Zielfunktion lautet:

max z = 20 x_{1} + 30 x_{2}

mit den Nebenbedingungen


$3 x_{1}$	+	$6.0 x_{2}$	$\leq$	$150.0$
$x_{1}$	+	$0.5 x_{2}$	$\leq$	$22.0$
$x_{1}$	+	$x_{2}$	$\leq$	$27.5$

.
und den Nicht-Negativitätsbedingungen

x_{1} \geq 0

und

x_{2} \geq 0

Graphisch: .

Abbildung 9: Lösungsraum der Ungleichung

Um die Ungleichungen besser verarbeiten zu können, werden Schlupfvariablen $y_{1} \geq 0$ , $y_{2} \geq 0$ und $y_{3} \geq 0$ eingeführt:


( $I_{1}$ )	$y_{1}$	$+$	$3 x_{1}$	$+$	$6.0 x_{2}$	$=$	$150.0$
( $I I_{1}$ )	$y_{2}$	$+$	$x_{1}$	$+$	$0.5 x_{2}$	$=$	$22.0$
( $I I I_{1}$ )	$y_{3}$	$+$	$x_{1}$	$+$	$x_{2}$	$=$	$27.5$

.
Die Schlupfvariable

y_{1}

sagt z.B. aus, wieviel kg Mehl nicht verbraucht wurde.
Das Gleichungssystem hat 3 Zeilen und 5 Variablen. Entsprechend sind 2 Variablen frei wählbar.
Das Prinzip des Simplex-Verfahrens besteht darin, ausgehend von einem Eckpunkt (einer Basislösung) zu einem weiteren Eckpunkt (ebenso eine Basislösung) und damit zu immer größeren Werten von z zu gelangen, bis ein weiteres Anwachsen nicht mehr möglich ist.

Die entsprechenden Schritte in diesem Beispiel sind:

1.

Erste zulässige Basislösung:

x_{1} = 0

x_{2} = 0

y_{1} = 150

y_{2} = 22

y_{3} = 27.5

ergibt

z = 0

2.

Verbesserung durch zunächst Festhalten von

x_{1} = 0

und Vergrößerung von

x_{2}

, da Zielfunktion dadurch am stärksten steigt:
Hierbei entstehen die Folgefragen:
a) Um wieviel kann

x_{2}

von 0 aus erhöht werden ?
b) Welche der Variablen

y_{1}

y_{2}

oder

y_{3}

sollen wir auf 0 setzen ?
Mit dem Versuch

y_{1} = 0

folgt aus (

I_{1}

), daß

x_{2} = 25

.
Mit dem Versuch

y_{2} = 0

folgt aus (

I I_{1}

), daß

x_{2} = 44

.
Mit dem Versuch

y_{3} = 0

folgt aus (

I I I_{1}

), daß

x_{2} = 27.5

. .
Damit ist der kritische Punkt in Gleichung (I), denn mit

x_{2} > 25

wird

y_{1} < 0

x_{2}

hat damit als Obergrenze den Wert 25.
Wir setzen also

x_{2} = 25

und damit

y_{1} = 0

3.

Neue Werte:

x_{1} = 0

x_{2} = 25

y_{1} = 0

y_{2} = 9.5

y_{3} = 2.5

ergibt

z = 750

4.

Umschreiben des Gleichungssystems, sodaß die Variablen, die nicht gleich Null gesetzt sind, durch die anderen Variablen ersetzt werden: .


( $I_{2}$ )	$x_{2}$	$=$	$25.0$	$-$	$\frac{1}{2} x_{1}$	$-$	$\frac{1}{6} y_{1}$
( $I I_{2}$ )	$y_{2}$	$=$	$9.5$	$-$	$\frac{3}{4} x_{1}$	$+$	$\frac{1}{12} y_{1}$
( $I I I_{2}$ )	$y_{3}$	$=$	$2.5$	$-$	$\frac{1}{2} x_{1}$	$-$	$\frac{1}{6} y_{1}$

z = 20 x_{1} + 30 x_{2} = 20 x_{1} + 30 \cdot (25 - \frac{1}{2} x_{1} - \frac{1}{6} y_{1})

z = 750 + 5 x_{1} - 5 y_{1}

5.

weitere Erhöhung von z durch Vergrößern von

x_{1}

(mit

y_{1}

wäre das kontraproduktiv; Deshalb

y_{1} = 0

a) Um wieviel kann $x_{1}$ von 0 aus erhöht werden ?
b) Welche der Variablen $x_{2}$ , $y_{2}$ oder $y_{3}$ sollen wir auf 0 setzen ?
Mit dem Versuch $x_{2} = 0$ folgt aus ( $I_{2}$ ), daß $x_{1} = 50$ .
Mit dem Versuch $y_{2} = 0$ folgt aus ( $I I_{2}$ ), daß $x_{1} = \frac{38}{3}$ .
Mit dem Versuch $y_{3} = 0$ folgt aus ( $I I I_{2}$ ), daß $x_{1} = 5$ . .
Damit ist der kritische Punkt durch Gleichung ( $I I I_{2}$ ) gegeben, und $x_{1}$ hat damit als Obergrenze den Wert 5.

6.

Neue Werte:

x_{1} = 5

x_{2} = 22.5

y_{1} = 0

y_{2} = 5.75

y_{3} = 0

ergibt

z = 775

7.

Umschreiben des Gleichungssystems, sodaß die Variablen, die nicht gleich Null gesetzt sind, durch die anderen Variablen ersetzt werden: .


( $I_{3}$ )	$x_{1}$	$=$	$5.0$	$+$	$\frac{1}{3} y_{1}$	$-$	$2 y_{3}$
( $I I_{3}$ )	$x_{2}$	$=$	$22.5$	$-$	$\frac{1}{3} y_{1}$	$+$	$y_{3}$
( $I I I_{3}$ )	$y_{3}$	$=$	$5.75$	$-$	$\frac{1}{6} y_{1}$	$+$	$\frac{3}{2} y_{3}$
	$z$	$=$	$775$	$-$	$\frac{10}{3} y_{1}$	$-$	$10 y_{3}$

8.

Der Versuch, eine weitere Erhöhung von

z

durch Vergrößern von

y_{1}

oder

y_{2}

von Null aus zu erreichen, führt nicht zum Ziel. Ergebnis:

x_{1} = 5

x_{2} = 22.5

z = 775

Lösung mit Maple:

with(simplex):
cnsts := {3*x+6*y ¡= 150, x+0.5*y ¡= 22, x+y ¡= 27.5}:
obj := -x+y+2*z:
maximize(obj, cnsts $\cup$ 0 ¡= x, 0 ¡= y, 0 ¡= z) oder:
maximize(obj, cnsts, NONNEGATIVE)oder:
maximize(obj, cnsts)
.

Beispiel 3 - 49 lp0190
Lösen Sie mit dem Simplex-Verfahren das Optimierungsproblem:
$max z = 3 x_{1} + 4 x_{2}$
$3 x_{1} + 2 x_{2} \leq 6$
$x_{1} + 4 x_{2} \leq 4$

PICT .

Abbildungsverzeichnis

1 Eingespannter Balken
2 Kräfte an einem Balken
3 Gleichungssystem als Excel-Tabelle
4 Rang einer Matrix
5 eine / unendlich viele / keine Lösungen
6 Lösbarkeit von Gleichungssystemen
7 Wechselverhalten der Getränkekonsumenten
8 Leslie-Diagramm
9 Lösungsraum der Ungleichung

Literatur

[PapulaF1] Papula: Formelsammlung,ISBN 978-3-8348-0757-1

[StoeckerF1] Stöcker : Taschenbuch mathematischer Formeln und moderner Verfahren, ISBN I978-3-8171-1700-0

[PapulaL1] Papula: Mathematik für Ingenieure und Naturwissenschaftler Band 1, ISBN 978-3-8348-0545-4

[PapulaL2] Papula: Mathematik für Ingenieure und Naturwissenschaftler Band 2, ISBN 978-3-8348-0564-5

[PapulaU1] Papula: Mathematik für Ingenieure und Naturwissenschaftler Klausur- und Übungsaufgaben, ISBN 978-3-8348-0609-3

[TurturU1] Turtur: Prüfungstrainer Mathematik, ISBN 978-3-8351-0023-8

[HoffmannL1] Hoffmann, Mathematik f. Ingenieure, Band 1, ISBN: 978-3-8273-7113-3

[HofmannL2] Hoffmann, Mathematik f. Ingenieure, Band 2, ISBN: 978-3-8273-7114-0

[WestermannL1] Westermann: Mathematische Probleme lösen mit Maple, ISBN 978-3540-77720-5

[RiessingerL1] Rießinger, Mathematik für Ingenieure, Springer-Verlag, ISBN 978-3540-89205-2

[HibbelerL1] Russel C. Hibbeler, Technische Mechanik I, Pearson-Verlag, ISBN 978-8273-7101-0

[Wiskowski] Wiskowski, Pharmakokinetik, http://www.meduniwien.ac.at/user/wolfgang.wyskovsky/homepage/h_texte/vortraege_praesentationen/TheoretischePharmakokinetik/Pharmakokinetik-Seiller.pdf

[Langguth] Langguth, Fricker, Wunderli-Allenspach, Biopharmazie, Wiley-VCH, ISBN 3-527-30455-X

[Croft] Croft, Mathematics for Engineers MyMathLab Global Pack, Prentice-Hall,ISBN: 978-1408263235

[Wikipedia_tVert] http://de.wikipedia.org/wiki/Studentsche_t-Verteilung

[Wikipedia_Box] http://de.wikipedia.org/wiki/Box-Whisker-Plot

[PapulaL3] Papula: Mathematik für Ingenieure und Naturwissenschaftler Band 3, ISBN 978-3-8348-1227-8

[Wikipedia_nVert] http://de.wikipedia.org/wiki/Normalverteilung

[Wikipedia_Chi-QuadratVert] http://de.wikibooks.org/wiki/Mathematik:_Statistik:_Tabelle_der_Chi-Quadrat-Verteilung

[Wikipedia_Weibull] http://de.wikipedias.org/wiki/Weibull-Verteilung

[HeSa] Hedderich, Sachs: Angewandte Statistik, Springer 2012, ISBN 978-3-642-24400-1

Mathematik für PharmazeutInnen . eine Einführung

Inhaltsverzeichnis

1 Reelle Matrizen

1.1 Einstieg: Lineare Gleichungssysteme

1.1.1 gängige Methoden

1.1.2 Einige Beispiele zum Einstieg

1.1.3 Lösen von Gleichungssystemen über äquivalente Umformungen

1.1.4 Übungen

1.1.5 Definition einer reellen Matrix

1.1.6 Transponierte einer Matrix

1.1.7 Gleichheit von Matrizen

1.2 Spezielle quadratische Matrizen

1.2.1 Diagonalmatrix

1.2.2 Dreiecksmatrix

1.2.3 Symmetrische Matrix

1.2.4 Schiefsymmetrische Matrix

1.3 Rechenoperationen mit Matrizen

1.3.1 Addition

1.3.2 Multiplikation mit einem Skalar

1.3.3 Multiplikation von Matrizen

1.3.4 Übungen

1.4 Gauß’scher Algorithmus

1.4.1 Darstellung in Matrixform

1.4.2 Lösungsschritte des Gauß’schen Algorithmus

1.4.3 Gauß-Jordan-Verfahren

2 Determinanten

2.1 Einstieg

2.1.1 zweireihige Determinanten

2.1.2 allgemeine Rechenregeln für Determinanten

2.2 Determinanten von Matrizen höherer Ordnung

2.2.1 Dreireihige Determinanten

2.2.2 Laplace’scher Entwicklungssatz

2.2.3 Determinanten höherer Ordnung

2.2.4 Lösbarkeit von Gleichungssystemen

2.2.5 Reguläre Matrix

2.2.6 Inverse Matrix

2.2.7 Übungen

2.2.8 Orthogonale Matrix

2.2.9 Rang einer Matrix

2.2.10 Anwendungen auf Lineare Gleichungssysteme

2.2.11 Lösungsverhalten eines linearen (m,n)-Gleichungssystems

2.2.12 Übungen

2.2.13 Lösung linearer Gleichungssysteme mit der Cramer’schen Regel

2.2.14 Auswirkungen von Rundungsfehlern

3 Anwendungen

3.1 Anwendungen in der Ökologie, Eigenwerte und Eigenvektoren

3.1.1 Markov-Ketten und Übergangsmatrizen

3.1.2 Leslie-Diagramme und Leslie-Matrizen

3.1.3 Eigenwerte und Eigenvektoren

3.2 Mischungen

3.2.1 Bestimmung von Zutatenmengen

3.3 Produktionsprozesse

3.3.1 Matrizen zur Beschreibung von Produktionsprozessen

3.3.2 Übungen

3.4 lineare Un-Gleichungssysteme

3.4.1 Lineare Optimierung

Abbildungsverzeichnis

Literatur

Mathematik für PharmazeutInnen .
eine Einführung