Eine Vogelpopulation bestehe zu Beginn aus 47 Jungvögeln und aus 55 Altvögeln. Die Wahrscheinlichkeit, dass ein Jungvogel nach drei Monaten immer noch ein Jungvogel ist, beträgt `w_1=0.1`. Die Wahrscheinlichkeit, dass er zu einem Altvogel wird, beträgt `w_2=0.8`. Außerdem ist die Wahrscheinlichkeit, dass ein Altvogel diesen Zeitraum überlebt, `w_3=0.8`. Jeder Altvogel sorgt mit einer Wahrscheinlichkeit von `w_4=0.6` dafür, dass in dieser Zeit ein neuer Jungvogel schlüpft.
Im folgenden Schaubild sind die Übergangswahrscheinlichkeiten aufgeführt:


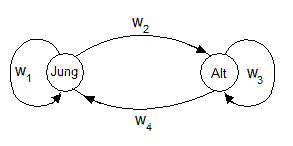
Stellen Sie zunächst die Leslie-Matrix auf, wenn der Populationsvektor die Form `v=((47),(55))` hat: Wie sieht die Population nach drei Monaten aus? Berechnen Sie die Eigenwerte der Matrix `A` (auf 2 Nachkommastellen gerundet und mit Komma getrennt):
`lambda_(12)=`

Wird diese Vogelpopulation (in dem Model) überleben, wenn die Übergangswahrscheinlichkeiten gleich bleiben?