
Beweis. Wir beweisen hier nicht alle diese Eigenschaften, sondern greifen uns nur einige als Beispiele heraus. Die verbleibenden Behauptungen werden durch ähnliche Überlegungen gezeigt. Zur Erinnerung sei noch einmal erwähnt, daß und .
(0). I(10) besagt: II(3) liefert oder
Wäre , so erhielte man aus II(4):
Folglich wäre Aus II(5) erhält man dann (mit Hilfe von Satz 2.1)
Also und
Aus II(3)
folgt dann
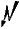 ! (zu I(10))
! (zu I(10))
(1). (Beweis indirekt.)
Angenommen, es gibt ein mit
Nach Definition gilt:
Da stets falsch ist, ist
auch die Konjunktion
und damit auch
stets falsch. 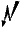 !
!
(5). Teil 1: Sei und .
Man hat zu zeigen, daß .
Es genügt zu zeigen: und . Es gilt und Aus folgt: , also Wegen gilt dann: und somit nach II(4)
Es bleibt noch zu zeigen:
Annahme,
Wegen existiert folglich ist
also im Widerspruch zu
Den 2. Teil der Behauptung (5) beweist man analog.
(7). Sei , also .
Folglich ist und daher
Also .
Angenommen: .
Dann gilt
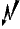 !
!
Die Umkehrung beweist man analog.
(11). Sei , dann ist nach (10) auch . Wegen gibt es nach dem archimedischen Axiom eine natürliche Zahl , so daß . Analog gibt es eine natürliche Zahl , so daß . Nach (10) erhält man daraus