
Beweis. (Der Beweis erfolgt mit einer sog. Würfelschachtelung, die analog zu einer Intervallschachtelung induktiv konstruiert wird). Beweisidee: Es sei und unendlich und beschränkt. Dann läßt sich in eine Kugel und damit auch in einen -dimensionalen Würfel mit endlicher Kantenlänge einschließen, wobei und für Es gilt also Die Kanten des Würfels werden durch die Intervalle auf den Koordinatenachsen repräsentiert (vgl. Abb. 6.4).
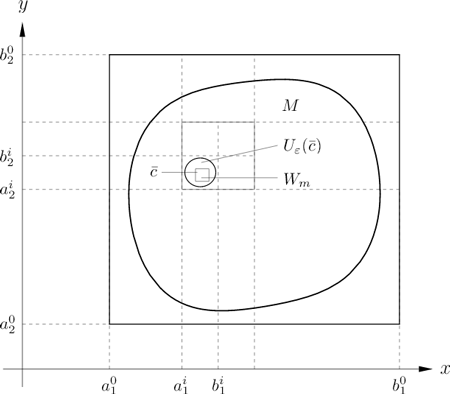

Durch Halbierung der Würfelkanten entsteht eine Zerlegung von in endlich viele Teilwürfel (in unserem Fall ist ) und . Dann ist
unendlich. Folglich gibt es einen Teilwürfel so daß schon unendlich ist. Wir wählen einen solchen Teilwürfel aus und nennen ihn . Es sei jetzt schon definiert mit den fogenden Eigenschaften: Die Kantenlänge von ist und ist unendlich. Analog wie bei halbieren wir jetzt die Kanten von und erhalten eine Zerlegung von in Teilwürfel , so daß
und
Da nach Voraussetzung unendlich ist, existiert ein so daß unendlich ist; sei .
Auf diese Weise entsteht eine Folge von ineinander geschachtelten Würfeln. Für den Würfel sei die -te Würfelkante () durch das Intervall gegeben. Offenbar ist dann eine Intervallschachtelung in . Nach dem Intervallschachtelungsaxiom gibt es ein so daß für fixiertes mit und
Behauptung: ist ein Häufungspunkt von .
Offenbar ist
.
Sei
. Wegen
kann mit wachsendem
die Kantenlänge
des
-ten
Würfels
so klein gemacht werden, daß für hinreichend große
der ganze
Würfel
zu
gehört:
.
Da
und
unendlich ist,
liegen in
unendlich
viele Elemente aus
folglich ist
ein
Häufungspunkt von
