
Beispiel: Sei und
Als Wurzelfunktion ist in stetig. Da beschränkt und abgeschlossen ist, ist in auch gleichmäßig stetig.
Angenommen, ist in Lipschitz-stetig.
Dann gibt es ein , so daß für alle Insbesondere für und beliebig gilt:
Also und damit
für alle
. Schließlich
folgt
für alle
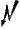 !
!