Wir führen jetzt die komplexen Zahlen ein, um sie für die Behandlung von sog. Potenzreihen zur Verfügung zu haben.

Wir setzen als bekannt voraus, daß $IR\times IR:={IR}^2$ einen zweidimensionalen Vektorraum mit den folgenden Operationen bildet:

     $\left(a,b\right)+\left(c,d\right)\text{:=}\left(a+c,b+d\right)$ (Addition von Elementen aus ${IR}^2$),

     $c\cdot \left(a,b\right)\text{:=}\left(ca,cb\right)$ (Multiplikation mit reellen Zahlen).

Zur geometrischen Veranschaulichung der komplexen Zahlen betrachten wir in ${IR}^2$ die kanonische Basis $\left\{\left(1,0\right),\left(0,1\right)\right\}$ und erhalten so ein rechtwinkliges Koordinatensystem für ${IR}^2$, mit dessen Hilfe sich die Elemente aus ${IR}^2$ als Punkte in der Ebene darstellen lassen $($Gaußsche Zahlenebene$)$.

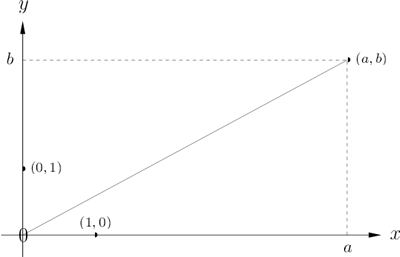
Jedes $\left(a,b\right)\in {IR}^2$ läßt sich eindeutig als Linearkombination der Basis darstellen. Die folgenden Teilmengen $\left\{\left(x,0\right):x\in IR\right\}$ und $\left\{\left(0,y\right):y\in IR\right\}$ bilden wichtige eindimensionale Teilräume, die mit den entsprechenden Koordinatenachsen identifiziert werden können.