Satz 5.6 $($ Zwischenwertsatz oder Nullstellensatz von Bolzano $)$ Ist $f$ in dem abgeschlossenen Intervall $[a, b]$ stetig und $f (a) < 0 < f (b)$ oder $f (a) > 0 > f (b)$ (d.h., $f (a) \cdot f (b) < 0$ ), dann gibt es ein $c \in (a, b)$ , so daß $f (c) = 0 .$

Beweis. Es sei o.B.d.A. $f (a) < 0 < f (b)$ (sonst wird $- f (a) < 0 < - f (b)$ betrachtet).

PICT

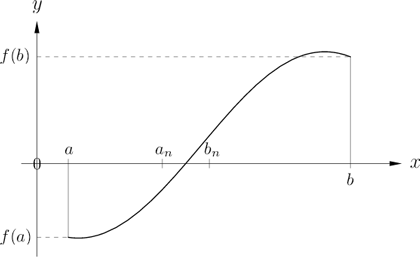
Wir konstruieren eine Intervallschachtelung $[a_{n}, b_{n}]$ , so daß

$f (a_{n}) < 0 \leq f (b_{n})$ und $b_{n} - a_{n} = \frac{1}{2^{n}} (b_{0} - a_{0}) .$

Sei $a_{0} : = a, b_{0} : = b \Rightarrow f (a) < 0 \leq f (b) .$ Für $n$ sei $[a_{n}, b_{n}]$ schon definiert (mit den geforderten Eigenschaften). Sei $c_{n + 1} = \frac{a_{n} + b_{n}}{2};$ dann definieren wir

$a_{n + 1} = a_{n}, b_{n + 1} = c_{n + 1},$ falls $f (c_{n + 1}) \geq 0$ und

$a_{n + 1} = c_{n + 1}, b_{n + 1} = b_{n},$ falls $f (c_{n + 1}) < 0$ .

Offenbar ist $(a_{n})$ monoton wachsend und nach oben beschränkt und $(b_{n})$ monoton fallend und nach unten beschränkt. Folglich existieren $lim a_{n}$ und $lim b_{n}$ , und wegen $b_{n} - a_{n} = \frac{1}{2^{n}} (b_{0} - a_{0})$ ist $lim a_{n} = lim b_{n} .$ Nach dem Intervallschachtelungsaxiom existiert ein $c$ mit $a_{n} \leq c \leq b_{n}$ für alle $n$ . $\Rightarrow lim a_{n} = c = lim b_{n} .$ Nach Voraussetzung ist $f (a_{n}) < 0 \leq f (b_{n})$ für alle $n$ . Da $f$ in $c$ stetig ist, gilt:

$f (c) = lim_{n \to \infty} f (a_{n}) \leq 0 \leq lim_{n \to \infty} f (b_{n}) = f (c)$

Daraus folgt also $f (c) = 0 .$ <mi
>P</mi><mi >I</mi><mi
>C</mi><mi >T</mi>