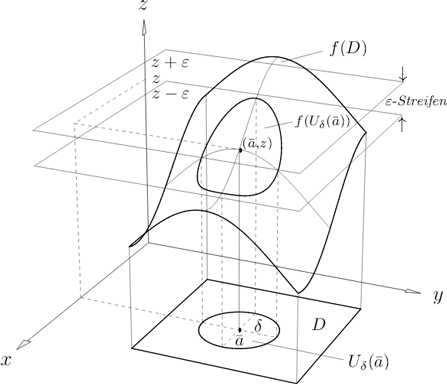
Definition. (Stetigkeit in metrischen Räumen) Sei $f:{IM}_1\to {IM}_2$ und $a\in {IM}_1$. $f$ ist in $a$ stetig =Df

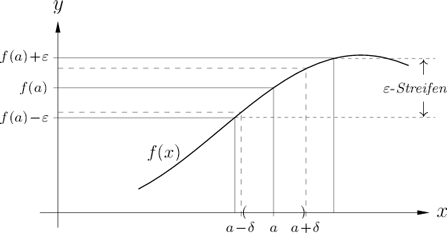
Wie für reellwertige Funktionen einer reellen Veränderlichen vereinbaren wir, daß eine Funktion $f$ in einer Menge $M\subseteq {IM}_1$ stetig ist, wenn sie in jedem Punkt der Menge stetig ist.

Ist z.B. ${IM}_1={IR}^n,{IM}_2=IR$ (mit dem euklidischen Abstand als Metrik) und ist $\overline{a}\in {IR}^n$, dann erhält man: $f$ ist in $\overline{a}$ stetig $\iff$ $\overline{a}\in D\left(f\right)$ und für jedes $\epsilon >0$ gibt es ein $\delta >0$, so daß für jedes $\bar{x}\in D\left(f\right)$ gilt: Wenn $|\bar{x}-\overline{a}|<\delta$, so $|f\left(\bar{x}\right)-f\left(\overline{a}\right)|<\epsilon$.