Satz 6.14 Es sei $f : {I R}^{n} \to I R$ und $M \subseteq {I R}^{n}$ . Ist $f$ in $M$ stetig, und ist $M$ beschränkt und abgeschlossen, dann ist auch $f (M)$ beschränkt und abgeschlossen.

Beweis. Wir zeigen zunächst, daß $f (M)$ beschränkt ist.

Angenommen, $f (M)$ ist nicht beschränkt. Dann gilt: Für jedes $c \in I R$ gibt es ein $\bar{x} \in M,$ so daß $| f (\bar{x}) | \geq c .$

Speziell für $c = c_{i} = i, i = 1, 2, 3, \dots$ existieren dann Elemente ${\bar{x}}_{1}, {\bar{x}}_{2}, {\bar{x}}_{3}, \dots \in M,$ so daß $| f ({\bar{x}}_{i}) | \geq c_{i} = i .$ Wegen ${\bar{x}}_{i} \in M$ ist die Folge $({\bar{x}}_{i})$ beschränkt, folglich besitzt $({\bar{x}}_{i})$ einen Häufungspunkt $\bar{a}$ und eine gegen $\bar{a}$ konvergente Teilfolge $({\bar{x}}_{i_{j}}) .$ Wenn ${\bar{x}}_{i_{j}} = \bar{a}$ für ein $j,$ dann ist $\bar{a} \in M .$ Wenn ${\bar{x}}_{i_{j}} \neq \bar{a}$ für alle $j,$ dann ist $\bar{a}$ ein Häufungspunkt der Menge ${{\bar{x}}_{i_{j}} : j = 0, 1, 2, \dots}$ , und damit ist auch $\bar{a} \in M,$ denn $M$ ist abgeschlossen. Folglich ist $f$ in $\bar{a}$ definiert und stetig. Wegen ${\bar{x}}_{i_{j}} \to \bar{a}$ gilt: $f ({\bar{x}}_{i_{j}}) \to f (\bar{a})$ . Andererseits ist $| f ({\bar{x}}_{i_{j}}) | \geq c_{i_{j}} = i_{j} \to \infty$ . Daher ist $(f ({\bar{x}}_{i_{j}}))$ unbeschränkt und somit nicht konvergent. 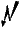PICT !

Wir zeigen nun, daß $f (M)$ abgeschlossen ist, d.h., ist $b$ ein Häufungspunkt von $f (M)$ , dann ist $b \in f (M) .$

Sei $b$ ein Häufungspunkt von $f (M)$ . Dann gibt es eine Folge $(b_{i})$ mit $b_{i} \in f (M)$ und $b_{i} \to b$ . Wegen $b_{i} \in f (M)$ gibt es ein ${\bar{x}}_{i} \in M$ , so daß $b_{i} = f ({\bar{x}}_{i})$ . Man erhält also eine Folge $({\bar{x}}_{i})$ in $M$ , die beschränkt ist, da ja $M$ beschränkt ist. Folglich besitzt $({\bar{x}}_{i})$ einen Häufungspunkt $\bar{a}$ und eine Teilfolge $({\bar{x}}_{i_{j}})$ , die gegen $\bar{a}$ konvergiert. Wie im ersten Teil des Beweises ist $\bar{a} \in M$ und damit $f (\bar{a}) \in f (M)$ , folglich ist $f$ in $\bar{a}$ stetig. Wegen ${\bar{x}}_{i_{j}} \to \bar{a}$ gilt: $b_{i_{j}} = f ({\bar{x}}_{i_{j}}) \to f (\bar{a}) = b \Rightarrow$

$f (\bar{a}) = b \in f (M) .$ <mi
>P</mi><mi
>I</mi><mi
>C</mi><mi
>T</mi>