Definition. (Sprungstelle bzw. Sprung) Sei $a$ ein Häufungspunkt von $D (f)$ . $f$ besitzt in $a$ einen Sprung (der Größe $d > 0$ ) =Df

f

besitzt in

a

einen rechtsseitigen Grenzwert

c_{r}

und einen linksseitigen Grenzwert

c_{l}

mit

c_{r} \neq c_{l}

(und

d = | c_{r} - c_{l} |

a

heißt dann auch Sprungstelle.

Ist z.B. $f (x) = {\begin{matrix} 1, für x \geq 0, \\ - 1, für x < 0, \end{matrix}$ dann besitzt $f$ an der Stelle $0$ einen Sprung der Größe 2. (vgl. Abb. 6.17)

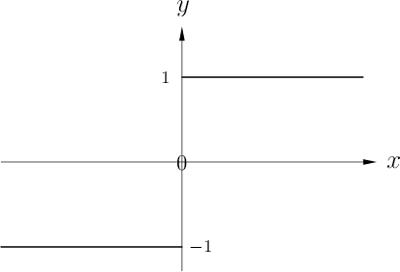
Abb. 6.17