Erklärungen
Wie Sie in den
letzten Kapitel ja wahrscheinlich schon gemerkt haben,
ist die Mathematik nach den Grundlagenthemen noch
lange nicht fertig - im Gegenteil: Sie hat noch viele
weitere Konzepte "vorrätig". In diesem Kapitel kommt
nun die Unterscheidung zwischen skalaren und
vektoriellen Größen hinzu. Das, was Sie bislang
kennengelernt haben, sind Skalare gewesen, nämlich
Maßzahlen evtl. zusammen mit einer Maßeinheit, z. B.
Längen, Zeiten oder Preise. Bei Vektoren kommt - wenn
man sie geometrisch interpretiert - zu der Maßzahl
noch die Angabe einer Richtung und einer Orientierung
hinzu, z. B. bei Geschwindigkeiten oder Kräften.
Gerade in der Physik (beispielsweise bei den
Bewegungsgleichungen Isaac Newtons) wird das Verstehen
schwierig, wenn man nicht weiß, was Vektoren sind und
wie man mit ihnen rechnet. Bei wirtschaftlichen
Betrachtungen sind Richtung und Orientierung zwar
meist eher unwichtig, trotzdem hat sich das Rechnen
mit Vektoren hier in vielen Fällen als sinnvoll und
praktisch herausgestellt.
Das Wort "Vektor" kommt aus dem Lateinischen und
bedeutet "Träger" oder "Passagier"; sprich: Es geht
darum, etwas von einem Ort zu einem anderen zu
transportieren, was dem gerade beschriebenen
physikalischen Verständnis von Vektoren nahe kommt.
Das Wort "Skalar" stammt - ebenso wie "Skala" und
"Skalierung" - vom lateinischen Wort "scala" ab,
welches "Leiter" oder "Treppe" bedeutet. Skalare
lassen sich also wie Treppenstufen anordnen. Dass man
in der Vektorrechnung lieber "Skalar" statt einfach
"Zahl" sagt, hat u. a. damit zu tun, dass sie sich
dadurch leichter von den Zahlen im Vektor, die ja eine
ganz andere "Aufgabe" haben, unterscheiden lassen.
Was ist ein Vektor?
Es gibt viele
Varianten, einen Vektor zu beschreiben: Die Spanne
reicht von der mathematisch-theoretischen Denkweise,
in der ein Vektor ein "Repräsentant eines
Vektorraumes" ist, bis zur anschaulichen Beschreibung
eines Vektors als Pfeil. Wir nutzen in diesem Kapitel
zwei Definitionen eines Vektors:
Komponentenweise:
Ein Vektor ist ein n-Tupel reeller
(oder auch komplexer)
Zahlen. Diese Zahlen nennt man die Komponenten des
Vektors. Man kann mithilfe eines Vektors also
mehrere Zahlen zu einem (mathematischen) Objekt
zusammenfassen und damit rechnen. In dieser Hinsicht
haben Vektoren eine gewisse Ähnlichkeit mit Tabellen,
die ja auch strukturierte Zusammenstellungen von
Zahlenwerten sind.
Man unterscheidet dabei Zeilenvektoren
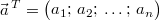 und Spaltenvektoren
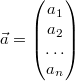 . Um einen
Zeilenvektor zu kennzeichnen, verwendet man das
hochgestellte 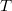 ,
welches für transponiert
steht und Zeilen und Spalten gegeneinander tauscht.
Für die geometrische Interpretation ist es im Großen
und Ganzen egal, welche "Version" des Vektors man
verwendet. Man kann sich hierbei also einfach die
bequemere Schreibweise aussuchen. Bei der Durchführung
von Rechenoperationen ist die Entscheidung schon
wichtiger. Dazu werden wir weiter unten kommen.
Aus der Definition eines n-Tupels leiten sich zwei
Dinge ab:
- n gibt
an, aus wie vielen Komponenten der Vektor besteht.
- Die
Reihenfolge der Komponenten ist wichtig. Die
Vertauschung von Komponenten erzeugt einen anderen
Vektor!
Für die Anschauung sind 2- und 3-komponentige
Vektoren, also Vektoren in der Ebene und im Raum,
praktisch. In der Mathematik, in der man sich ja
(bekanntermaßen) an fehlender Anschauung nicht sehr
stört, kann man problemlos auch mit n-komponentigen
Vektoren arbeiten. Das Schöne dabei ist, dass sich an
den Grundprinzipien nichts ändert. Im nächsten
Abschnitt wird es dazu ein Beispiel geben.
Geometrisch:
Der Pfeil, durch den der Vektor symbolisiert wird,
zeichnet sich durch drei Angaben aus, die in gleicher
Weise für den Vektor von Bedeutung sind: seine Länge,
seine Richtung und seine Orientierung, wobei
Orientierung meint, an welcher Seite des Pfeils die
Pfeilspitze ist.
Damit ist schon ganz schön viel über einen Vektor
festgelegt. Wichtig ist aber auch, was nicht festgelegt
ist: Auch wenn Anfangs- und Endpunkt eines Vektors
durchaus eine Rolle spielen können, sind sie im
Allgemeinen unerheblich. Das heißt: Der Begriff
"Vektor" bezeichnet nicht einen
Pfeil, sondern viele, nämlich
all diejenigen, die die gleiche Länge, gleiche
Richtung und gleiche Orientierung haben. Falls Ihnen
das komisch vorkommt: Letztendlich ist es bei Brüchen
ganz ähnlich: 
und 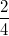
sehen zwar unterschiedlich aus, meinen aber die
gleiche Zahl.
Auf der linken Seite der folgenden Grafik sehen Sie
fünf Pfeile, die alle die gleiche Länge, die gleiche
Richtung und die gleiche Orientierung haben. Es ist
also ein Vektor
dargestellt. Anfangs- und Endpunkt spielen dabei keine
Rolle. Die Pfeile auf der rechten Seite unterscheiden
sich hinsichtlich Länge, Richtung und/oder
Orientierung. Hier sind also vier verschiedene
Vektoren symbolisiert.
Um von der
Komponenten- zur grafischen Darstellung zu kommen und
umgekehrt, braucht man - wie schon an anderen Stellen
- ein Koordinatensystem.
Das 2-achsige Koordinatensystem,
welches wir bislang für Funktionen verwendet haben,
hilft allerdings nur weiter, wenn die Vektoren zwei
Komponenten haben. Haben die Vektoren drei
Komponenten, benötigt man entsprechend ein
Koordinatensystem mit drei Achsen. Mit Vektoren mit
mehr als drei Komponenten lässt sich zwar problemlos
rechnen. Da es mit der Anschauung dann aber sowieso
nicht mehr funktioniert, brauchen wir uns auch keine
Gedanken über ein passendes Koordinatensystem zu
machen...
Wie funktioniert das nun konkret: Betrachten wir zwei
Punkte (der Einfachheit halber in der Ebene, sodass
wir 2-komponentige Vektoren bekommen) 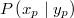 und 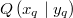 . Möchte man von
 zu 
gelangen, muss man sich 
Einheiten in x-Richtung und 
Einheiten in y-Richtung bewegen. Damit haben wir auch
schon den entsprechenden Vektor berechnet. Man erhält
also einen Vektor aus seinem Anfangs- und Endpunkt,
indem man die Koordinaten des Anfangspunkts von den
Koordinaten des Endpunkts subtrahiert.
Man schreibt dafür 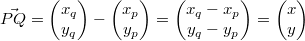
Dieser Vektor 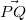
trägt zwar noch die Punkte im Namen, sagt aber
letztendlich nur aus, dass man 
Schritte in x-Richtung und 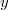
Schritte in y-Richtung gegangen ist. Damit haben wir
den Kreis geschlossen zu der Aussage, dass ein Vektor
nicht einen, sondern viele Pfeile bezeichnet. Dass
diese Pfeile alle die gleiche Länge, gleiche Richtung
und gleiche Orientierung haben, ist nicht so
überraschend, weil sie ja alle aus den Komponenten  und 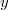
bestehen.
Ein Beispiel:
Die Grafik rechts zeigt, wie aus den Punkten 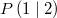 und 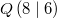 der Vektor 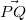
berechnet wird: 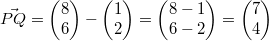
Eine Folgerung:
Zwei Vektoren 
und 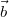
sind dann gleich, wenn sie die gleiche Anzahl Zeilen
bzw. Spalten haben und alle Komponenten gleich sind.
Man schreibt in diesem Fall: 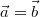 bzw. 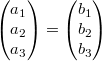
Umgekehrt bedeutet das, dass zwei Vektoren dann
verschieden sind, wenn sie sich in mindestens einer
Komponente unterscheiden. Es müssen nicht alle
Komponenten unterschiedlich sein; eine reicht völlig.
Stellen Sie sich das geometrisch vor: Bereits die
Veränderung einer Komponente reicht, damit die
Richtung und/oder Länge des Vektors anders ist.
Noch
etwas Formales: Es gibt verschiedene
Varianten, wie man Vektoren bezeichnet.
In diesem Kapitel werden kleine Pfeile über der
(lateinischen) Variablenbezeichnung
oder Pfeile über dem Anfangs- und Endpunkt des Vektors
verwendet. In anderen Texten werden auch halbfette
Buchstaben (was handschriftlich eher unpraktisch ist)
oder Unterstriche zur Kennzeichnung verwendet. In
alten Mathebüchern findet man auch altdeutsche
Frakturbuchstaben als Bezeichnung. Es kommt -
mathematisch gesehen - nicht darauf an. Hauptsache,
die Bezeichnungen sind eindeutig und einheitlich.
Erste
Rechenoperationen mit Vektoren
Wie bei vielen
mathematischen Größen möchte man auch bei Vektoren
wissen, wie man mit ihnen rechnet - sonst würde man ja
nicht viel mit ihnen anfangen können...
Eine
Einschränkung zu Beginn: Nicht alle diese
Rechenoperationen sind in allen
Anwendungszusammenhängen wirklich sinnvoll und
aussagekräftig. Sie zu definieren ist natürlich
trotzdem wichtig, um an den richtigen Stellen richtig
mit ihnen umgehen zu können. Auch bei Skalaren führt
ja nicht jede Rechnung automatisch zu einer
brauchbaren Aussage. Beispiel: Die Feststellung, dass
alle Professorinnen und Professoren einer Hochschule
zusammen 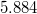
Jahre alt sind, lässt sich nicht sinnvoll
interpretieren. Die Aussage, dass das
durchschnittliche Alter der Professorinnen und
Professoren 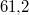
Jahre ist, ist hingegen für die Personalplanung eine
wichtige Größe.
Ebenso muss man auf die Einheiten aufpassen - und auch
hier ist es bei Skalaren genauso: 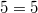
ist sicher richtig. 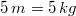
passt weder von den Einheiten zusammen noch lassen
sich sinnvolle Aussagen daraus ableiten.
Hier nun das oben versprochene
Beispiel:
Der Zeilenvektor 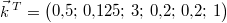 bezeichne das
Rezept eines Rührkuchens: 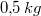
Mehl, 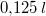
Milch, 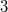
Eier, 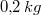
Butter, 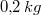
Zucker und 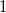
Päckchen Backpulver. Auch wenn man Kuchenrezepte in
Realität natürlich nicht als Vektor abbildet, lassen
sich an diesem Beispiel einige Dinge gut
veranschaulichen:
- Wir
haben damit (ohne große Probleme) einen
6-komponentigen Vektor erzeugt. Wie oben gesagt:
Ein Vektor ist erstmal "nur" eine Zusammenstellung
von Werten. Man kann den Vektor
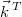 zwar nicht
zeichnen, verstehen kann man ihn trotzdem. zwar nicht
zeichnen, verstehen kann man ihn trotzdem.
- Die
Einheiten sind in diesem Vektor genauso wichtig
wie sonst: Ändert man den Vektor zu
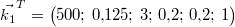 , sollte man
dazu sagen, dass die Mehlmenge jetzt in Gramm
angegeben ist. Mit , sollte man
dazu sagen, dass die Mehlmenge jetzt in Gramm
angegeben ist. Mit 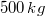 Mehl wird der Kuchen sicher nichts...
Mehl wird der Kuchen sicher nichts...
- Auch das
Vertauschen von Komponenten geht nicht einfach so:
Den Vektor
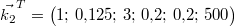 muss man in
diesem Zusammenhang interpretieren als: muss man in
diesem Zusammenhang interpretieren als: 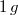 Mehl, Mehl, 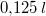 Milch,
Milch, 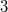 Eier,
Eier, 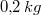 Butter,
Butter, 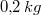 Zucker und
Zucker und 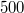 Päckchen Backpulver. Ich denke, das spricht für
sich...
Päckchen Backpulver. Ich denke, das spricht für
sich...
Addition und
Subtraktion
Voraussetzung
dafür, dass Vektoren addiert
werden können, ist, dass alle Vektoren gleich viele
Komponenten haben. Gleiches gilt (natürlich) für die
Subtraktion.
In den Formeln dieses Kapitels werden bloß Vektoren
mit 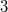
Komponenten betrachtet. Für Vektoren mit 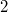 , 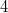 oder mehr
Komponenten funktionieren die Konzepte genauso.
Damit die Vektoren ordentlich gezeichnet werden
können, wurden für die Beispiele 2-komponentige
Vektoren gewählt.
Addition
Komponentenweise:
Die Summe
zweier Vektoren 
und 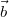
berechnet man, indem man die Komponenten der beiden
Vektoren zeilenweise addiert, also 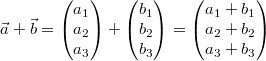 Geometrisch:
Geometrisch:
Geometrisch verschiebt man bei der Addition
von zwei Vektoren 
und 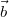
den zweiten Vektor 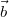
parallel, sodass sein Anfangspunkt im Endpunkt von 
liegt. Der Summenvektor führt dann vom Anfangspunkt
von 
zum Endpunkt von 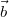 .
In der Schreibweise mit Anfangs- und Endpunkt ergibt
sich daraus die folgende Gleichung:
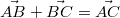 .
Da das entstehende Dreieck zu
einem Parallelogramm
ergänzt werden kann, kann man auch sagen: Der
Summenvektor ist die Diagonale des Parallelogramms,
das aus den Vektoren gebildet wird.
Beispiel:
Gegeben seien 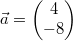 und 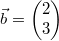 . Dann ist 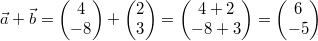
Hier die zugehörige Grafik:
Bei der Addition
von mehr als zwei Vektoren erweitert man dieses
Verfahren einfach, also: Anfangspunkt des zweiten
Vektors an Endpunkt des ersten, Anfangspunkt des
dritten Vektors an Endpunkt des zweiten, Anfangspunkt
des vierten Vektors an Endpunkt des dritten, ... und
verbindet den Anfangspunkt des ersten Vektors mit den
Endpunkt des letzten - fertig. Dabei kann es
passieren, dass der Endpunkt des letzten Vektors genau
auf dem Anfangspunkt des ersten Vektors liegt. Die
Summe aller dieser Vektoren ist dann 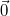 . Dass man in
Formelschreibweise einfach die entsprechenden
Komponenten der einzelnen Vektoren - egal wie viele es
sind - addiert, versteht sich fast von selbst...
Zwei ganz wichtige Vektoren in diesem Zusammenhang:
- Der Nullvektor:
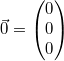 .
Geometrisch gesehen, bildet der Nullvektor einen
Punkt auf sich selbst ab und ist daher der einzige
Vektor, für den die Veranschaulichung durch einen
Pfeil nicht funktioniert. Bitte achten Sie darauf,
dass .
Geometrisch gesehen, bildet der Nullvektor einen
Punkt auf sich selbst ab und ist daher der einzige
Vektor, für den die Veranschaulichung durch einen
Pfeil nicht funktioniert. Bitte achten Sie darauf,
dass 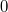 (ein Skalar) und
(ein Skalar) und 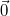 (ein Vektor, bestehend aus mehreren Werten) zwei
völlig unterschiedliche Gebilde sind.
(ein Vektor, bestehend aus mehreren Werten) zwei
völlig unterschiedliche Gebilde sind.
- Der Gegenvektor:
Zu einem Vektor
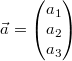 ist ist 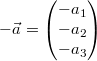 der
sogenannte Gegenvektor. Geometrisch betrachtet,
hat der
sogenannte Gegenvektor. Geometrisch betrachtet,
hat 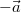 die gleiche Länge und die gleiche Richtung wie
die gleiche Länge und die gleiche Richtung wie  ,
aber die entgegengesetzte Orientierung. Anders
gesagt, wenn ,
aber die entgegengesetzte Orientierung. Anders
gesagt, wenn  von Punkt
von Punkt 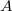 zu Punkt
zu Punkt 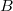 verläuft, verläuft
verläuft, verläuft 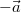 von
von 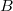 zu
zu 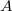 . .
Subtraktion
Wie beim "normalen Rechnen" ist auch bei Vektoren die
Subtraktion die Umkehrung der Addition. Das macht die
Sache einfach:
Komponentenweise:
Die Differenz
zweier Vektoren berechnet man, indem man die
Komponenten der beiden Vektoren zeilenweise subtrahiert,
also 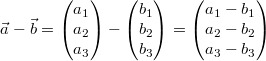
Wenn man möchte, kann man das - ähnlich wie bei ganzen
Zahlen - als Addition des Gegenvektors
verstehen: 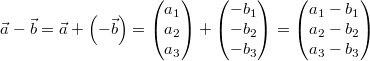 . Das Ergebnis
ist natürlich dasselbe.
Geometrisch:
Der Gedanke mit dem Gegenvektor liefert einen guten
Einstieg für die geometrische Variante von  : Da 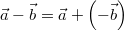 , verschiebt man
den Gegenvektor von 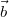
so, dass sein Anfangspunkt im Endpunkt von  liegt. Der
Differenzvektor führt dann vom Anfangspunkt von 
zum Endpunkt von 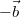 .
Alternativ kann man sich die Frage stellen, welcher
Vektor zu 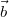
addiert werden muss, damit 
herauskommt - auch diese Überlegung kennt man vom
Rechnen mit Skalaren.
Beispiel:
Gegeben seien wieder 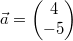 und 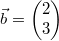 . Dann ist 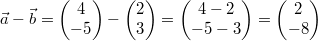
Hier die zugehörige Grafik:
Da sich Addition
und Subtraktion von Vektoren direkt auf die Addition
und Subtraktion von reellen Zahlen
zurückführen lassen, gelten hier die gleichen Rechengesetze,
z. B. Kommutativ- und
Assoziativgesetz. Das heißt, Vektoren verhalten
sich hier angenehmerweise so, wie man es gewohnt ist.
Skalare
Multiplikation
Eine Bemerkung
vorweg: Aus Gründen, die wahrscheinlich
keine/r mehr wirklich benennen kann, bezeichnet man
Skalare in der Vektorrechnung gerne mit griechischen
Buchstaben, am liebsten mit 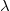
(gesprochen: lambda) oder 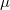
(gesprochen: mü). Geschickt ist das auf jeden Fall,
weil dadurch Verwechslungen zwischen Skalaren und
Vektoren vermieden werden.
Komponentenweise:
Ein Vektor 
wird mit dem Skalar 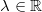 multipliziert
multipliziert, indem jede
Komponente des Vektors mit dem Skalar multipliziert
wird, also 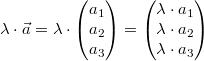 Bemerkung
1:
Bemerkung
1: Den Multiplikationspunkt  darf man - wie
bei der "normalen" Multiplikation - weglassen, wenn
die Schreibweise eindeutig bleibt.
Bemerkung
2: Ebenfalls wie bei der "normalen"
Multiplikation kann man die skalare Multiplikation
dafür nutzen, "unhandliche" Faktoren vorzuziehen. Ein
Beispiel: 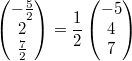 Geometrisch:
Geometrisch:
Die geometrische Interpretation der skalaren
Multiplikation eines Vektors 
mit dem Skalar 
ist nicht sehr überraschend: Die Länge des Vektors
ändert sich um den Faktor  . An der
Richtung ändert sich hingegen nichts. Eventuell wird
allerdings die Orientierung umgekehrt. Das
charakterisiert man mit folgenden Begriffen:
-
Multipliziert man einen Vektor
 mit einem positiven
Skalar mit einem positiven
Skalar 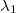 ,
so hat ,
so hat 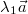 die gleiche Orientierung wie
die gleiche Orientierung wie  .
Die Vektoren .
Die Vektoren  und
und 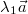 sind parallel
oder auch gleichsinnig parallel.
sind parallel
oder auch gleichsinnig parallel.
-
Multipliziert man einen Vektor
 mit einem negativen
Skalar mit einem negativen
Skalar 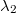 ,
so hat ,
so hat 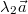 die entgegen gesetzte Orientierung von
die entgegen gesetzte Orientierung von  . Die
Vektoren . Die
Vektoren  und
und 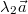 sind antiparallel
oder auch gegensinnig parallel. Die Multiplikation
mit
sind antiparallel
oder auch gegensinnig parallel. Die Multiplikation
mit 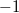 erzeugt den Gegenvektor.
erzeugt den Gegenvektor.
-
Multipliziert man einen Vektor mit
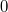 , entsteht der Nullvektor, was vermutlich wenig
überraschen wird... Anders ist es da schon mit der
Festlegung, dass der Nullvektor zu jedem Vektor
parallel ist. Dies ist nicht wirklich
offensichtlich, aber später in verschiedenen
Zusammenhängen nützlich.
, entsteht der Nullvektor, was vermutlich wenig
überraschen wird... Anders ist es da schon mit der
Festlegung, dass der Nullvektor zu jedem Vektor
parallel ist. Dies ist nicht wirklich
offensichtlich, aber später in verschiedenen
Zusammenhängen nützlich.
Parallele und antiparallele Vektoren lassen sich durch
Parallelverschiebung in eine Linie bringen. Sie heißen
deshalb auch kollinear
(abgeleitet vom Lateinischen "collinearis": auf der
gleichen Gerade/Linie liegend).
Bis hierhin wurden in diesem Kapitel bloß Vektoren mit
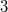
Komponenten betrachtet. Für Vektoren mit 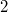 , 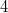
oder mehr Komponenten funktionieren die Konzepte
genauso. Auch hier noch zwei Beispiele mit
einem 2-komponentigen Vektor:
-
Parallelität: Gegeben seien
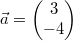 und und 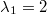 . Das
skalare Produkt ist . Das
skalare Produkt ist 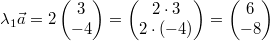
-
Antiparallelität: Gegeben seien
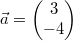 und und 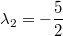 . Das
skalare Produkt ist . Das
skalare Produkt ist 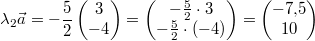
Hier das Ganze in einer Grafik:
Aus dem gleichen
Grund wie bei Addition
und Subtraktion
gelten auch hier das Kommutativ- und
das Assoziativgesetz sowie zusätzlich zwei
Varianten des Distributivgesetzes:
Für die Vektoren 
und 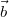
sowie die Skalare 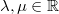 gelten
Was ist eine
Linearkombination?
Mit diesen gerade
besprochenen Rechenoperationen kann man schon eine
ganze Menge erreichen: Bereits mit zwei
2-komponentigen Vektoren kann man mithilfe von
Vektoraddition und skalarer Multiplikation eine
komplette Ebene erzeugen. Drei 3-komponentige
Vektoren und Vektoraddition und skalare
Multiplikation reichen für den 3-dimensionalen Raum.
Etwas formaler die folgende Vokabel:
Definition:
Verknüpft man mehrere n-komponentige Vektoren
mittels Addition und skalarer Multiplikation,
spricht man von einer Linearkombination.
In einer Formel: 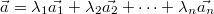 mit den
Skalaren 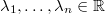 und den
n-komponentigen Vektoren 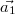
bis 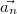 Wichtig:
Wichtig:
Eine Linearkombination von Vektoren ergibt wieder
einen Vektor. In diesem Fall ist das der Vektor 
Ein Beispiel:
Wir betrachten nochmal das Kuchenbeispiel von oben.
Ein Rezept für Nusskuchen lautet: 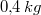 Mehl, 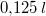 Milch, 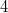 Eier, 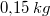 Butter, 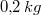
Zucker, 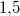
Päckchen Backpulver und 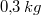
Nüsse. Dieses Rezept lässt sich durch den Vektor 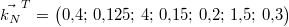 darstellen.
Damit der Vektor 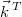
des Rührkuchens die gleiche Anzahl an Komponenten
hat, müssen wir als letzte Komponente eine 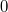 ergänzen, denn
Nüsse sind ja nicht enthalten: 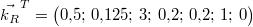 . Bitte
beachten Sie, dass der Rührkuchenvektor einen
anderen Namen bekommen hat! Da nur Vektoren, die die
gleiche Anzahl von Komponenten haben, identisch sein
können, gilt: 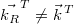
Nun lässt sich mithilfe einer Linearkombination
bestimmen, wie viele Zutaten vorhanden sein müssen,
wenn 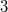
Nusskuchen und 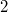
Rührkuchen gebacken werden sollen, nämlich:

Man benötigt also insgesamt 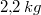
Mehl, 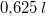
Milch, 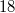
Eier, 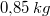
Butter, 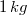
Zucker, 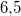
Päckchen Backpulver und 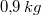
Nüsse.
Zugegebenermaßen hätte man das auch ohne
Vektorrechnung problemlos ausrechnen können. Das
Beispiel soll auch nur zeigen, dass sich hinter dem
Begriff "Linearkombination" kein wirklich
schwieriges Konzept versteckt...
Der Betrag eines
Vektors
Definition:
Der Betrag eines Vektors

ist ein Maß für seine Länge oder - wenn man es
anschaulich möchte - ein Maß für die Länge des Pfeils.
Wie bei Zahlen schreibt man dafür: 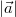 Komponentenweise:
Komponentenweise:
Bei der Berechnung hilft uns ein "alter Bekannter",
nämlich der Satz des
Pythagoras. Daraus ergeben sich die folgenden
Formeln: 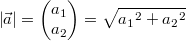 für
2-komponentige Vektoren, 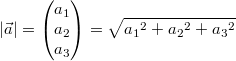 für
3-komponentige Vektoren bzw. 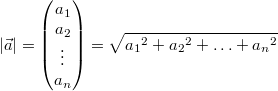 für den
allgemeinen Fall.
Aufgrund der Wurzeleigenschaften
ist der Betrag eines Vektors natürlich immer größer
oder gleich 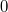 .
Ist ja für eine Länge auch logisch... Weil die
einzelnen Komponenten unter der Wurzel quadriert
werden, gilt 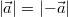 Geometrisch:
Geometrisch:
Damit haben wir
gleichzeitig erklärt, wo diese Formeln herkommen -
zumindest für den 2-dimensionalen Fall...
Ein geometrischer Anwendungsfall:
Um von zwei gegebenen Vektoren 
und 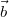
den Abstand ihrer Endpunkte zu bestimmen, rechnet man:
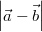
bzw. 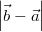
. Da sich 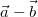
und 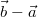
nur im Vorzeichen unterscheiden, das ja durch den
Betrag ohnehin wegfällt, ist es egal, welche Differenz
man bildet.
Und
nun ein Beispiel:
Gegeben sei 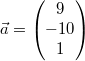
Der Betrag dieses Vektors ist 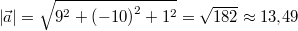
Statt vom "Betrag des Vektors" wird auch von der " Norm
des Vektors" gesprochen. Statt 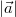 schreibt man
dann 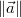
. Das Konzept der "Norm" ist in der höheren Mathematik
von größerer Bedeutung, als hier vielleicht deutlich
wird. Schon mal gut zu wissen ist, dass normierte Vektoren,
sprich Vektoren, die den Betrag 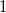
haben, häufig nützlich sind. Um einen beliebigen
Vektor 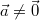
zu normieren, muss man diesen Vektor mit dem Kehrwert
seines Betrages skalarmultiplizieren, man rechnet
also: 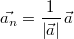 . Der
entstehende Vektor hat dieselbe Richtung und
Orientierung wie  ,
aber eben den Betrag 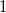 .
Im oberen Beispiel würde das so aussehen: 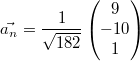
Lineare
Unabhängigkeit
Ein wichtiges
Konzept bei Vektoren, das es so bei Zahlen nicht gibt,
ist die Lineare Unabhängigkeit.
Definition:
Die Vektoren 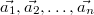 heißen linear unabhängig,
wenn die Gleichung 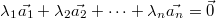 nur die Lösung
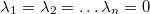
hat.
Anders gesagt: Eine Linearkombination dieser Vektoren
ergibt nur dann den
Nullvektor, wenn alle skalaren Koeffizienten 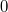 sind.
Und noch eine andere Formulierung: Keiner der Vektoren
lässt sich aus den anderen kombinieren.
Definition:
Die Vektoren 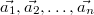 heißen linear abhängig,
wenn die Gleichung 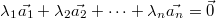 mehrdeutig
lösbar mehrdeutig
lösbar ist. Das heißt, wenn die Gleichung nicht
nur die Lösung 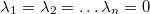 hat, sondern es
noch weitere Lösungen gibt.
Anders gesagt: Eine Linearkombination dieser Vektoren
ergibt auch dann den
Nullvektor, wenn nicht alle
skalaren Koeffizienten 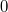
sind.
Und auch hier noch eine andere Formulierung:
Mindestens einer dieser Vektoren ist eine
Linearkombination der übrigen Vektoren, lässt sich
also mithilfe der anderen darstellen.
Ein
Merksatz zur linearen Unabhängigkeit:
Die Anzahl der Komponenten gibt vor, wie viele linear
unabhängige Vektoren es maximal geben kann: in der
Ebene zwei, im Raum drei. Die Vektoren 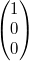 , 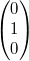 und 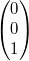 (Man nennt sie
auch Einheitsvektoren.) sind das beste Beispiel dafür:
Es gibt keine weitere Möglichkeit, eine 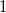 in einen
3-komponentigen Vektor "unterzubringen".
Wichtige Folgerung: Jeder weitere Vektor mit 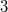 Komponenten
lässt sich eindeutig aus diesen erzeugen. Das ist
natürlich nicht bloß bei diesen speziellen Vektoren
so: Hat man drei linear unabhängige 3-komponentige
Vektoren, kann man damit jeden Vektor des
3-dimensionalen Raumes eindeutig darstellen.
Merksätze
zur linearen Abhängigkeit:
- Eine
Menge von Vektoren, die den Nullvektor enthält,
ist immer linear abhängig. Zur Verdeutlichung ein
Beispiel: Die Vektorgleichung
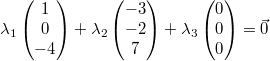 hat
unendlich viele Lösungen, z. B. hat
unendlich viele Lösungen, z. B.
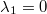 ,
, 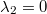 und
und 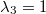
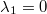 ,
, 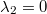 und
und 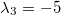
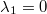 ,
, 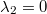 und
und 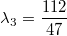 - oder
oder oder...
- Eine
Menge linear abhängiger Vektoren enthält sozusagen
"überflüssige" Informationen: Betrachtet man zwei
linear abhängige Vektoren, beispielsweise
 und und 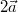 , kann man
mit ihnen sämtliche Punkte einer Geraden
darstellen. Das hätte man aber auch mit nur einem
der beiden Vektoren erreichen können. Zwei linear
unabhängige Vektoren spannen hingegen eine Ebene
auf. Man "gewinnt" also eine Dimension hinzu. Das
führt zu den folgenden beiden Aussagen: , kann man
mit ihnen sämtliche Punkte einer Geraden
darstellen. Das hätte man aber auch mit nur einem
der beiden Vektoren erreichen können. Zwei linear
unabhängige Vektoren spannen hingegen eine Ebene
auf. Man "gewinnt" also eine Dimension hinzu. Das
führt zu den folgenden beiden Aussagen:
- Zwei
Vektoren sind linear abhängig, wenn sie
parallel sind.
- Drei
Vektoren sind linear abhängig, wenn sie in
einer Ebene liegen. So, wie zwei parallele
Vektoren kollinear
heißen (siehe oben), heißen drei Vektoren, die
in einer Ebene liegen, komplanar
(abgeleitet vom Lateinischen "planum": in der
gleichen Ebene/Plane liegend).
Wie
stellt man nun fest, ob eine Menge von Vektoren
linear (un)abhängig ist?
Es ist leider so, dass es Vektoren meist nicht sofort
anzusehen ist, ob sie linear abhängig oder linear
unabhängig sind. Daher folgendes Verfahren: Man
betrachtet 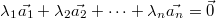 , also eine
Vektorgleichung mit den Variablen 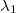
bis 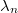 .
Daraus entsteht ein Lineares
Gleichungssystem, dessen Lösung Auskunft über
die Lineare (Un)Abhängigkeit der Vektoren gibt.
Hier der Rechenweg anhand von zwei Beispielen:
1.
Gegeben seien die drei Vektoren 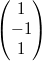 , 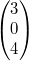 und 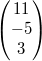
Um zu entscheiden, ob sie linear abhängig oder
unabhängig sind, muss die folgende Gleichung gelöst
werden: 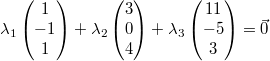
Diese führt zu dem Gleichungssystem:
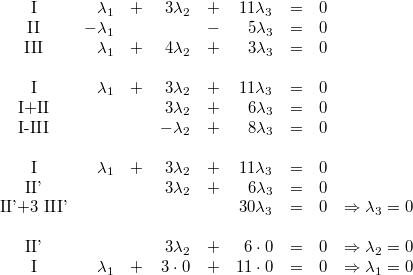 Ergebnis:
Ergebnis:
Da 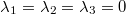
die einzige Lösung des Gleichungssystems ist, sind die
drei Vektoren linear unabhängig.
2.
Gegeben seien die drei Vektoren 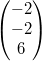 , 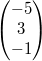 und 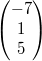
Um zu entscheiden, ob sie linear abhängig oder
unabhängig sind, muss die folgende Gleichung gelöst
werden: 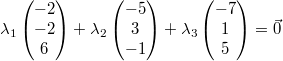
Diese führt zu dem Gleichungssystem:
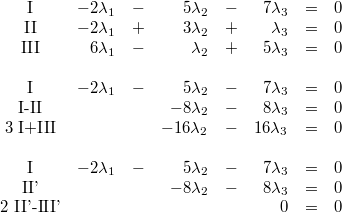
Wegen der entstandenen Nullzeile ist es offensichtlich
unmöglich, eine eindeutige Lösung zu finden. Es gibt
also unendlich viele Lösungen dieses
Gleichungssystems. Sprich: Zu jeder Variable, die wir
frei wählen, können wir die beiden anderen so
berechnen, dass das Gleichungssystem gelöst wird.
Nehmen wir z. B. 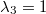
. Eingesetzt in 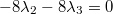 führt dies zu 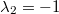
. Dies beides eingesetzt in die erste Gleichung ergibt
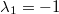
. Eine weitere Lösung (auf dem gleichen Weg berechnet)
ist 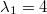
, 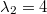
und 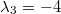
. Auch 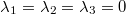
ist im Übrigen eine Lösung des Gleichungssystems -
aber eben nicht die einzige...
Ergebnis:
Da die Gleichung keine eindeutige Lösung hat, sind die
drei Vektoren linear abhängig. Ein Vektor lässt sich
also als Linearkombination der anderen darstellen, z.
B. ist 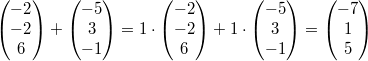 Eine
mathematische Randbemerkung:
Eine
mathematische Randbemerkung: Da auf den
rechten Seiten der Gleichungen jeweils eine 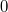 steht
(mathematisch nennt man so etwas ein homogenes
Lineares Gleichungssystem), gibt es hier nur zwei
Möglichkeiten für die Lösung: Entweder ist das
Gleichungssystem eindeutig lösbar mit der Lösung 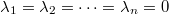
; dann sind die Vektoren linear unabhängig. Oder das
Gleichungssystem hat unendlich viele Lösungen; dann
sind die Vektoren linear abhängig.
Eine
lerntechnische Randbemerkung: Falls Sie mit
dem Lösen Linearer Gleichungssysteme Schwierigkeiten
haben, schauen Sie bitte im entsprechenden Kapitel
nach. Dort sind die verschiedenen Lösungswege
ausführlich erklärt - und Übungsaufgaben gibt es auch.
Ausblick:
Es gibt weitere Wege, um festzustellen, ob Vektoren
linear (un)abhängig sind, beispielsweise kann man
dafür auch Determinanten nutzen. Darum wird es in
einem späteren Kapitel gehen.
Produkte von Vektoren
Bei der
Multiplikation von Vektoren muss man ein bisschen
aufpassen: Anders als bei "normalen Zahlen"
unterscheidet man hier vier verschiedene Produkte!
Neben der skalaren Multiplikation, die oben schon
behandelt wurde ("Skalar mal Vektor gleich Vektor")
gibt es noch das Skalarprodukt ("Vektor mal Vektor
gleich Skalar"), das Vektorprodukt ("Vektor mal Vektor
gleich Vektor") und das Spatprodukt, bei welchem
Vektor- und Skalarprodukt verknüpft werden ("Vektor
mal Vektor mal Vektor gleich Skalar"). Diese Vielfalt
resultiert daraus, dass wir nicht mehr nur Objekte
gleichen Typs miteinander multiplizieren (also "eine
Zahl mal eine andere Zahl"), sondern nun verschiedene
mathematische Objekte zur Hand haben, nämlich Zahlen und
Vektoren, sodass sich einfach mehr
Kombinationsmöglichkeiten ergeben.
Ganz
wichtig: Eine Division
durch Vektoren ist nicht definiert! Möglich ist
allerdings, einen Vektor durch einen Skalar zu teilen
- das ist eine Folgerung aus der skalaren
Multiplikation, die ja die Multiplikation von Vektoren
mit Brüchen
nicht ausschließt.
Skalarprodukt
Wir beginnen mit
dem Skalarprodukt. Das Zeichen für diese
Rechenoperation ist 
, also der gleiche Multiplikationspunkt wie bei der
skalaren Multiplikation. Da man Skalar und Vektor aber
gut unterscheiden kann, ist das nicht das Problem. Ein
bisschen aufpassen sollte man trotzdem...
Man nennt das Skalarprodukt auch inneres Produkt oder
Punktprodukt.
Wichtig
vorab:
- Ein
Skalarprodukt kann man nur berechnen, wenn beide
Vektoren die gleiche Anzahl von Komponenten haben.
- Aus
Gründen, die später bei der Matrizenrechnung
wichtig werden, benötigen wir den ersten Faktor
als Zeilenvektor und den zweiten als
Spaltenvektor. Man sagt auch abkürzend:
"Zeilenvektor mal Spaltenvektor". In anderen
Lehrbüchern wird das Skalarprodukt auch als
"Spaltenvektor mal Spaltenvektor" notiert.
Rechnerisch macht das auch tatsächlich keinen
großen Unterschied, aber der Zusammenhang von
Skalarprodukt und Matrizmultiplikation wird nicht
so deutlich.
Definition:
Komponentenweise:
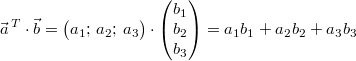 Geometrisch:
Geometrisch:
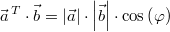
In Worten: Das Skalarprodukt ist das Produkt
der Beträge beider Vektoren und dem Kosinus
des kleineren Winkels zwischen 
und 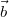
, hier 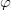
(gesprochen: "phi") genannt.
Wichtig:
Skalarprodukte können immer nur von genau zwei
Vektoren berechnet werden, denn das Ergebnis dieser
Multiplikation ist ja ein Skalar. Würde man dieses
Ergebnis mit einem weiteren Vektor multiplizieren
wollen, wäre die Ausgangssituation also nicht mehr
"Vektor mal Vektor".
Ein Beispiel:
Gegeben seien 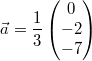 und 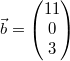
Das Skalarprodukt dieser beiden Vektoren ist 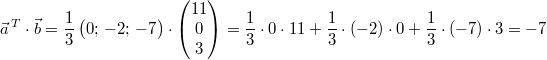
Solange wir mit dem Winkel zwischen zwei Vektoren noch
nichts anfangen können, hilft uns die geometrische
Variante nicht viel. Sie wird aber weiter unten
nützlich werden.
Rechengesetze beim
Skalarprodukt:
Die Skalarmultiplikation hat - netterweise - mehr oder
weniger die Eigenschaften einer "normalen"
Multiplikation, z. B. kann man einfach Klammer
ausmultiplizieren und das Kommutativ-
bzw. Assoziativgesetz anwenden.
Einen bedeutenden
Unterschied gibt es aber: Der Satz
vom Nullprodukt gilt hier nicht! Das heißt: Das
Skalarprodukt zweier Vektoren kann auch dann 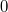 sein, wenn beide
Vektoren vom Nullvektor verschieden sind. Ein
Beispiel: 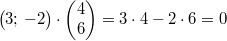 . Das ist
(vermutlich) zunächst überraschend, ergibt sich aber
direkt aus der geometrischen Form des Skalarprodukts:
Neben den Beträgen der Vektoren spielt ja auch der
Kosinus des eingeschlossenen Winkels eine Rolle. Und
der Kosinus von 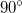
bzw. 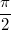
ist bekanntlich 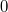 .
Geometrisch interpretiert: Die Vektoren stehen also
senkrecht (orthogonal) zueinander.
Zusammenfassung:
Das Skalarprodukt zweier Vektoren ist genau dann 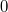 , wenn
(mindestens) einer der Vektoren der Nullvektor ist
oder die Vektoren einen rechten Winkel einschließen.
Dazu noch eine Vokabel: Ein Vektor, der im rechten
Winkel zu einem anderen Vektor (oder auf einem
sonstigen geometrischen Objekt) steht, heißt Normalenvektor.
Schauen wir noch an, was passiert, wenn man das Skalarprodukt
eines Vektors mit sich selbst berechnet: 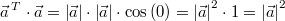 Ergebnis:
Ergebnis:
Das Skalarprodukt eines Vektors mit sich selbst ist
das Quadrat seines Betrages.
Zieht man daraus die Wurzel,
erhält man 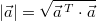 . Daraus folgt,
dass das Skalarprodukt eines Vektors mit sich selbst
immer dann größer als 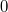
ist, wenn der Vektor nicht der Nullvektor ist. Wurzeln
aus positiven
Werten liefern ja bekanntlich positive Ergebnisse.
Ein Beispiel
Eine kleine Bemerkung vorab: Vektor 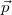 wird beim ersten
Auftreten nur deswegen als Zeilenvektor geschrieben,
weil er dann weniger Platz braucht...
Betrachten wir noch einmal das Rührkuchenbeispiel von
oben: 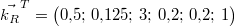 . Sind nun die
Kosten pro Kilogramm Mehl, Liter Milch, Ei, Kilogramm
Butter, Kilogramm Zucker und Päckchen Backpulver in
dem folgenden Vektor zusammengetragen 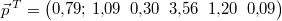 , liefert das
Skalarprodukt einen Weg, den Gesamtpreis des Kuchens
auszurechnen, nämlich:
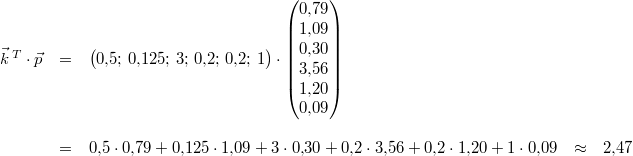
Die Zutaten für den Kuchen kosten insgesamt also etwa
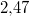
EUR.
Auch wenn man (verständlicherweise) fürs Kuchenbacken
normalerweise nicht die Vektorrechnung bemüht, sind
die hier aufgezeigten Prinzipien durchaus realistische
Anwendungsfälle. Ersetzt man den "Rezeptvektor" durch
einen allgemeinen Mengenvektor, ist der Weg vom
Kuchenbacken zur innerbetrieblichen
Leistungsverrechnung oder zur Produktionsplanung in
Unternehmen nicht weit.
Eine Anwendung des
Skalarprodukts: Die Berechnung von Winkeln zwischen
Vektoren
Ein geometrisches Konzept: Die Ermittlung des Winkels,
der von zwei Vektoren eingeschlossen wird.
Wichtig:
Dies ist natürlich nur dann sinnvoll möglich, wenn
beide Vektoren vom Nullvektor verschieden sind.
Dieser Winkel bzw. sein Kosinus
tauchte ja etwas weiter oben bereits auf, nämlich in
der Formeln 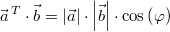 . Da es ja noch
eine zweite Variante gibt, das Skalarprodukt zu
berechnen, können wir die beiden Formeln kombinieren:
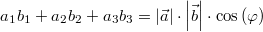
Nach ein bisschen Umstellen erhält man für die
Winkelberechung folgende Formel: 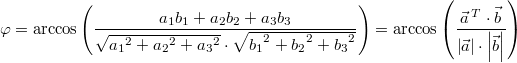
Dieser Winkel liegt zwischen 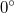
und 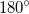
bzw. zwischen 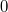
und 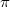 .
Zwei
Winkelbeispiele:
Betrachten wir nochmal das Beispiel von oben: 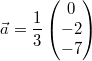 und 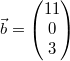
Das Skalarprodukt dieser beiden Vektoren ist (wie
bereits berechnet): 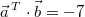
Um den Winkel zwischen diesen Vektoren zu bestimmen,
benötigen wir nun noch die Beträge:
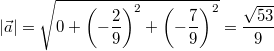
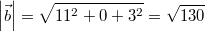
Der Winkel 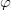
zwischen 
und 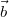
ist also: 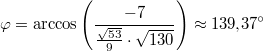
Und nun - damit wir das Ganze vernünftig zeichnen
können - noch ein Beispiel mit 2-komponentigen
Vektoren:
Gegeben seien die Vektoren 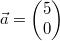 und 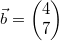
Das Skalarprodukt dieser beiden Vektoren ist: 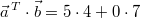
Um den Winkel zwischen diesen Vektoren zu bestimmen,
benötigen wir nun noch die Beträge:
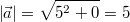
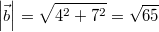
Der Winkel 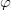
zwischen 
und 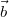
ist also: 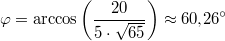
In einer Grafik sieht das dann so aus:
Vektorprodukt
Um das
Vektorprodukt vom Skalarprodukt unterscheiden zu
können, wird hier ein anderes Zeichen benutzt, nämlich

. Wegen dieses Zeichens wird das Vektorprodukt auch
Kreuzprodukt genannt. Manchmal nennt man es auch
äußeres Produkt. Die Bezeichnung "Vektorprodukt" gibt
aber - wie Skalarprodukt - von vorneherein ganz klar
an, wie das Ergebnis aussieht. Daher verwende ich hier
diesen Begriff.
Wichtig
vorab: Das Vektorprodukt gibt es in dieser
Form nur für dreidimensionale Vektoren!
Definition:
Komponentenweise:
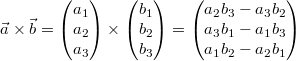
Das sieht zunächst reichlich verwirrend aus... Um sich
die Formel zu merken, gibt es eine Eselsbrücke,
die auch Schnürsenkelprinzip genannt wird:
Dazu schreibt man 1. die Komponenten der beiden
Vektoren jeweils zweimal untereinander, streicht als
2. die erste und die letzte Zeile und subtrahiert dann
als 3. die entstehenden Produkte über Kreuz: Es werden also in
jeder Zeile des Ergebnisses genau die anderen Zeilen
der Ausgangsvektoren verknüpft: in der ersten
Ergebniszeile die Elemente aus der 2. und 3. Zeile der
Ausgangsvektoren etc. Zudem unterscheiden sich Minuend
und Subtrahend
im Ergebnis nur durch die Reihenfolge der Indizes.
Später werden Sie noch eine Möglichkeit kennenlernen,
Vektorprodukte zu berechnen - allerdings muss man dazu
mit Determinanten umgehen können.
Geometrisch:
Vom geometrischen Standpunkt aus ist es ja immer
wichtig, von einem Vektor Betrag, Richtung und
Orientierung zu kennen. Da das Vektorprodukt nun mal
einen Vektor als Ergebnis liefert, müssen diese Fragen
auch hier beantwortet werden:
Der Betrag des Vektorprodukts entspricht der Fläche
des Parallelogramms,
das von 
und 
aufgespannt wird, also: 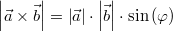 , wobei 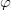 der kleinere
Winkel ist, der zwischen 
und 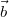
liegt.
Zu Richtung und Orientierung: 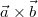 steht im rechten
Winkel zu 
und 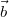 .
Zusammen bilden die Vektoren  ,
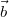
und ihr Vektorprodukt ein so genanntes Rechte-Hand-System,
in dem sich 
, 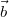
und 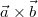
wie Daumen, Zeigefinger und Mittelfinger der rechten
Hand verlaufen. Damit ist dann auch die Orientierung
festgelegt.
Ein Rechenbeispiel:
Gegeben seien 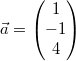 und 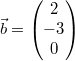
Das Vektorprodukt dieser Vektoren ist 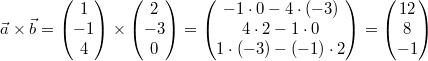 Anwendung:
Anwendung:
Physiker bzw. Ingenieure nutzen Vektorprodukte
beispielsweise, um die Feldstärke von Magnetfeldern zu
bestimmen. In der BWL kommt man üblicherweise ohne
Vektorprodukte aus.
Spatprodukt
Kommen wir zum
letzten Produkt von Vektoren: Da das Spatprodukt eine
Kombination aus Skalar- und Vektorprodukt ist, wird
meist keine eigenes Symbol dafür eingeführt. Man nennt
das Spatprodukt (aus leicht einsehbaren Gründen) auch
gemischtes Produkt.
Wichtig
vorab 1: Da ein Vektorprodukt berechnet wird,
müssen die Vektoren jeweils drei Komponenten haben.
Wichtig
vorab 2: Da ein Skalarprodukt berechnet wird,
ist das Ergebnis ein Skalar.
Definition:
Komponentenweise:
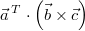
Bitte achten Sie darauf, dass die Klammern genau so
gesetzt werden müssen. 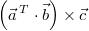 würde nicht
funktionieren, weil 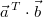 ja einen Skalar
als Ergebnis hat. Aus diesem Skalar und dem Vektor 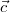
kann aber kein Vektorprodukt berechnet werden.
Geometrisch:
In den geometrischen Betrachtungen steckt gleichzeitig
die Erklärung, was man mit dem Spatprodukt anfangen
kann. Dafür müssen wir zunächst die Frage klären, was
ein Spat im mathematischen Sinne (man sagt dazu auch
Parallelepiped) ist: Es handelt sich um ein Art
dreidimensionales Parallelogramm,
das von drei Vektoren im Raum aufgespannt wird (siehe
Grafik rechts). Mithilfe des Spatprodukts kann man das
Volumen eines solchen Spats bestimmen: 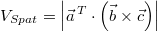 . Es fügt sich
in dieser Hinsicht gut an das Vektorprodukt an, mit
dem ja die Fläche eines Parallelogramms berechnet
werden kann. Und wie beim Vektorprodukt spielt auch
hier die Orientierung eine Rolle, wenn wir auf den
Betrag verzichten: Ist das Spatprodukt positiv, bilden

, 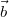
und 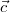
(in dieser Reihenfolge) ein Rechtssystem. Ist das
Spatprodukt negativ, bilden 
, 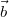
und 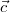
(in dieser Reihenfolge) ein Linkssystem. Man spricht
daher auch vom orientierten Volumen
(ähnlich dem orientierten Flächeninhalt bei Integralen).
Ein Beispiel:
Gegeben seien 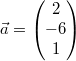 ,  und 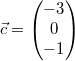
Das Spatprodukt dieser Vektoren ist 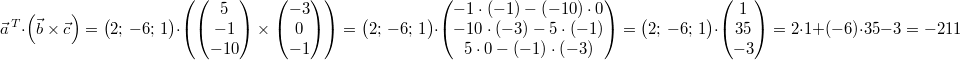
Rechengesetze beim
Spatprodukt:
- Da das
Vektorprodukt eines Vektors mit sich selbst der
Nullvektor und das Skalarprodukt eines beliebigen
Vektors mit dem Nullvektor
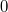 ist, ist auch
ist, ist auch 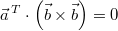
- Dass das
Spatprodukt nicht kommutativ
ist, ist relativ naheliegend, weil das
Vektorprodukt es ja auch nicht ist. Allerdings
gibt es hier stattdessen eine wirklich spannende
Eigenschaft: Der Wert des Spatprodukts ändert sich
nicht, wenn man die Faktoren zyklisch
durchtauscht:
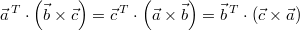
- Ebenso
wie das Vektorprodukt ist das Spatprodukt nicht assoziativ.
Eine Art Assoziativgesetz gilt aber für Skalare:
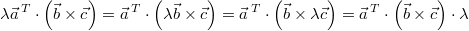 . Anders
formuliert: Multipliziert
man einen der Vektoren mit einem Skalar, kann man
diesen quasi aus dem Spatprodukt "ausklammern". . Anders
formuliert: Multipliziert
man einen der Vektoren mit einem Skalar, kann man
diesen quasi aus dem Spatprodukt "ausklammern".
Einen Sonderfall
müssen wir noch betrachten, nämlich 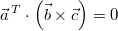 . Dann muss das
Volumen des betrachteten Spats 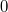
sein, was entweder passiert, wenn einer der Vektoren
der Nullvektor ist oder die drei Vektoren in einer
Ebene liegen (dann kann ja kein 3-dimensionales
Gebilde entstehen). Das heißt, man kann mithilfe des
Spatprodukts feststellen, ob drei gegebene Vektoren komplanar
(in anderen Worten: linear abhängig) sind. Dieser
Rechenweg ist manchmal einfacher, als der im Abschnitt
"Lineare Unabhängigkeit" beschriebene.
Ausblick
Mathematisch kann
man eine Menge mit Vektoren machen, das überhaupt
nichts mehr mit Geometrie und Pfeilen zu tun hat. Das
ist ja durchaus typisch für die Mathematik: Hat man in
einem Bereich etwas Nützliches gefunden, sucht man
nach Möglichkeiten, dieses Prinzip auf andere Bereiche
zu übertragen.
Der ganz oben erwähnte Vektorraum ist ein Beispiel
dafür: Ausgehend von Vektoren wurde ein (abstraktes)
Konzept entwickelt, welches u. a. auf Funktionen
angewendet werden kann. Das klingt zunächst vielleicht
komisch, ist aber sehr praktisch. Wurde nämlich
gezeigt, dass eine Menge von Funktionen einen
Vektorraum bildet, weiß man, dass die Funktionen
bestimmte Eigenschaften haben (müssen) und dass
bestimmte Rechenverfahren problemlos angewendet werden
können. Man muss dies also nicht für jede Eigenschaft
und jedes Rechenverfahren einzeln überprüfen.
Etwas naheliegender sind natürlich Matrizen und
Determinanten. Diese können beispielsweise beim Lösen
Linearer Gleichungssysteme,
die ja in vielen Zusammenhängen auftreten, eingesetzt
werden. Darauf baut z. B. auch der Simplex-Algorithmus
zum Lösen Linearer Optimierungsprobleme auf. Nach
vielen militärischen Anwendungsfällen wird dieses
Verfahren heute im Rahmen des Operations Research vor
allem in Unternehmen eingesetzt, um herauszufinden,
wie die gegebenen Mittel eingesetzt werden müssen, um
das beste aller möglichen Ergebnisse zu erreichen.
Sie sehen, das Feld, in dem Vektoren zum Einsatz
kommen, ist vielfältig. Damit Sie Vektoren später für
die eigentlich spannenden Dinge nutzen können, wurden
in diesem Kapitel die Grundlagen gelegt, ohne die es -
wie immer - nicht geht.
|
 Brückenkurs
Brückenkurs