| Figure 20: Schwerpunkt eines Viertelkreises |
in9025
Berechnung des Schwerpunkts eines Viertelkreises: .
Bleibt man hier in der Darstellung kartesischer Koordinaten, wird die Berechnung wesentlich aufwendiger, wie das Beispiel für die y-Koordinate zeigt: .

Figure 20: Schwerpunkt eines Viertelkreises
.
 .
.
 .
.
.
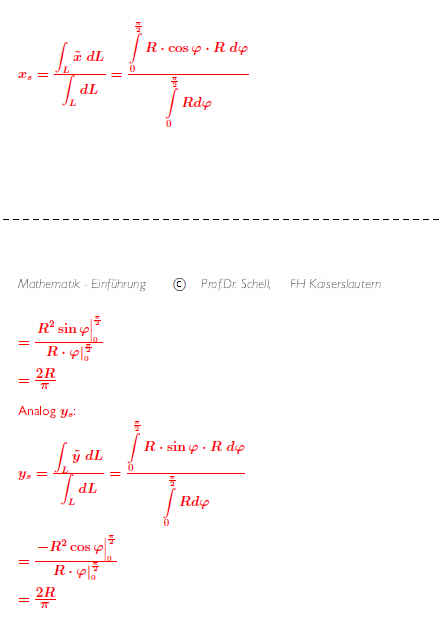
Eine alternative Berechnung geht wie folgt: Wir zerteilen den Kreisbogen (willkürlich) in lauter kleine Kreissegmente
dL = R · dϕ. .
Hier sind die Integralgrenzen einfach angebbar, sie liegen zwischen 0 und π/2. .
Haben wir die Schwerpunkte der einzelnen kreissegmente, können wir den Schwerpunkt des Viertelkreises daraus bestimmen. .

Figure 21: Schwerpunkt eines Viertelkreises
.
Der Schwerpunkt eines einzelnen Stückchens liegt bei x = R · cosϕ bzw. ỹ = R · sinϕ .
Damit erhält man einen Ausdruck für den Schwerpunkt eines Viertelkreisbogens: .
.
.
Lösung: .