BAYES Theorem
Für zwei Ereignisse 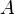 und
und 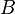 mit
mit 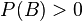 lässt sich die Wahrscheinlichkeit von
lässt sich die Wahrscheinlichkeit von
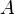 unter der Bedingung, dass
unter der Bedingung, dass 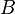 eingetreten ist, angeben durch die Wahrscheinlichkeit von
eingetreten ist, angeben durch die Wahrscheinlichkeit von
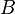 unter der Bedingung, dass
unter der Bedingung, dass 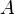 eingetreten ist:
eingetreten ist:
-
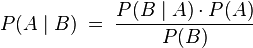 .
.
Hierbei ist
-
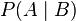 die (bedingte) Wahrscheinlichkeit des Ereignisses
die (bedingte) Wahrscheinlichkeit des Ereignisses 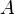 unter der Bedingung, dass
unter der Bedingung, dass 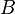 eingetreten ist,
eingetreten ist, -
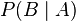 die (bedingte) Wahrscheinlichkeit des Ereignisses
die (bedingte) Wahrscheinlichkeit des Ereignisses 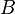 unter der Bedingung, dass
unter der Bedingung, dass 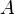 eingetreten ist,
eingetreten ist, -
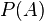 die A-priori-Wahrscheinlichkeit des Ereignisses
die A-priori-Wahrscheinlichkeit des Ereignisses 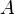 und
und -
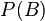 die A-priori-Wahrscheinlichkeit des Ereignisses
die A-priori-Wahrscheinlichkeit des Ereignisses 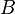 .
.
Endlich viele Ereignisse:
Wenn 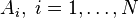 eine Zerlegung der Ergebnismenge in disjunkte Ereignisse ist, gilt für die A-posteriori-Wahrscheinlichkeit
eine Zerlegung der Ergebnismenge in disjunkte Ereignisse ist, gilt für die A-posteriori-Wahrscheinlichkeit 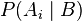
-
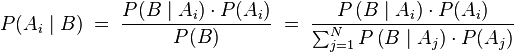 .
.
Den letzten Umformungsschritt bezeichnet man auch als Marginalisierung.
Da ein Ereignis 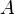 und sein Komplement
und sein Komplement 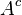 stets eine Zerlegung der Ergebnismenge darstellen, gilt insbesondere
stets eine Zerlegung der Ergebnismenge darstellen, gilt insbesondere
-
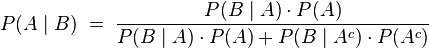 .
.