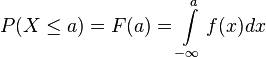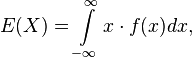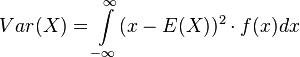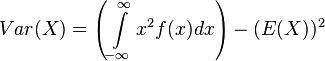stetige Zufallsvariablen

Eine stetige Zufallsvariable kann in jedem beschränkten Intervall unendlich viele Ausprägungen annehmen.

Ihre Verteilung lässt sich durch eine Dichtefunktion f(x) beschreiben.

(f(x) ist hier keine Wahrscheinlichkeit, sondern eine Dichte !)

Verteilungsfunktion

$P(X \le a)= F(a) = \int\limits_{-\infty}^{a}f(x)dx$

• Es gilt: P(X = a) = 0.

• Wegen P(X = a) = 0 ist P(X ≤ a) = P(X < a) und P(X > a) = P(X ≥ a)

Die Dichtefunktion f(x) ist die erste Ableitung der Verteilungsfunktion, falls diese an der Stelle x differenzierbar ist.

• Die Dichtefunktion f(a) kann auch größer als 1 werden.

• Ausgehend von 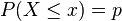$P(X \le x) = p$ ist das p-Quantil x(p) der Wert x, der zu einer gegebenen Wahrscheinlichkeit p gehört. Speziell x(0,5) ist der Median.

Erwartungswert

$E(X) = \int\limits_{-\infty}^{\infty} x \cdot f(x) dx ,$

falls E(X) existiert, d.h. nicht unendlich wird.

Varianz

$Var(X) = \int\limits_{-\infty}^{\infty} (x-E(X))^2 \cdot f(x) dx$

wobei auch hier der Verschiebungssatz angewendet werden kann:

$Var(X) = \left(\int\limits_{-\infty}^{\infty} x^2 f(x) dx \right) - (E(X))^2$