Test auf Anteilswert (Binomialtest)
Der Anteilswert θ wird geschätzt durch
-
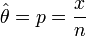 .
.
Mit dem Binomialtest können folgende Hypothesenpaare für θ getestet werden:
| Test |  |  |
|---|---|---|
| zweiseitig | 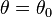 | 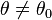 |
| rechtsseitig | 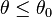 | 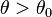 |
| linksseitig | 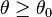 | 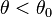 |
- für n > 30 , nθ0 ≥ 10 n(1-θ0) ≥ 10
- kann man durch die Gauß-Verteilung approximieren:
- Testfunktion
-
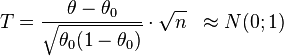 (Gauß-Test) .
(Gauß-Test) .
| Ablehnungsbereich | |
|---|---|
| zweiseitig | 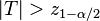 |
| rechtsseitig | 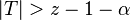 |
| linksseitig | 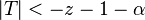 |
- für n < 30 oder nθ0 < 10 oder n(1-θ0) < 10
- ist der exakte Binomialtest anzuwenden:
- Testfunktion
Die Teststatistik  gibt an, wie oft das Merkmal in einer zufälligen Stichprobe vom Umfang
gibt an, wie oft das Merkmal in einer zufälligen Stichprobe vom Umfang  aufgetreten ist.
aufgetreten ist.
Unter der Nullhypothese 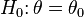 ist die Teststatistik
ist die Teststatistik 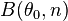 -verteilt, das heißt
-verteilt, das heißt
-
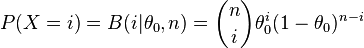 .
.
- Ablehnungsbereich
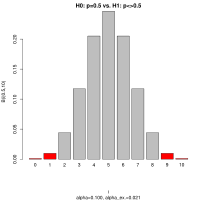
Da die Teststatistik diskret verteilt ist, kann das vorgegebene Signifikanzniveau 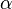 in der Regel nicht eingehalten werden.
in der Regel nicht eingehalten werden.
Daher wird gefordert, die kritischen Werte so zu wählen, dass für ein möglichst großes exaktes Signifikanzniveau 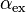 gilt
gilt 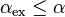 .
.
Für den zweiseitigen Test werden daher als kritische Werte das größte 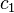 und das kleinste
und das kleinste 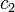 bestimmt, für die gilt
bestimmt, für die gilt
-
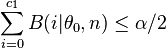 und
und -
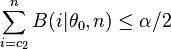 .
.
Das exakte Signifikanzniveau ergibt sich als
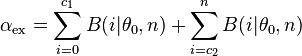 .
.
Für die beiden einseitigen Tests wird analog verfahren.
| Test | Kritische Werte | Kritischer Bereich | Grenze(n) |
|---|---|---|---|
| zweiseitig | 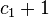 und und 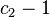 | 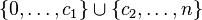 | |
| rechtsseitig | 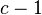 | 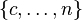 | c = kleinster Wert, für den 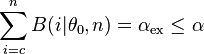 |
| linksseitig | 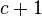 | 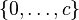 | c = größter Wert, für den 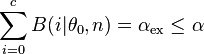 |