Test auf Varianz
| Test | 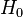 | 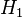 |
|---|---|---|
| zweiseitig | 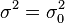 | 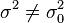 |
| rechtsseitig | 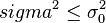 | 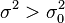 |
| linksseitig | 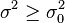 | 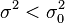 |
1. X ist normalverteilt, μ ist unbekannt, n beliebig
- Testfunktion
-
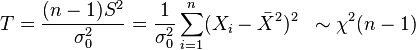
| Ablehnungsbereich | |
|---|---|
| zweiseitig | 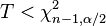 oder oder 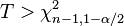 |
| rechtsseitig | 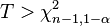 |
| linksseitig | 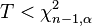 |
2. X ist normalverteilt, μ ist bekannt, n beliebig
- Testfunktion
-
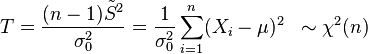
| Ablehnungsbereich | |
|---|---|
| zweiseitig | 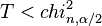 oder oder 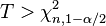 |
| rechtsseitig | 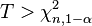 |
| linksseitig | 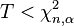 |