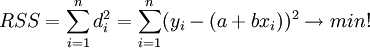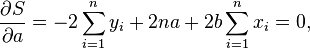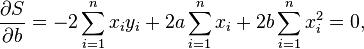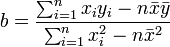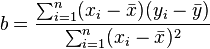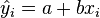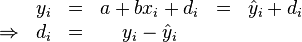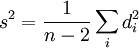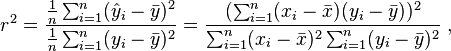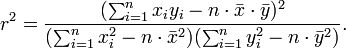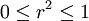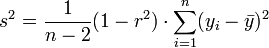Lineare Regression
mittels der Methode der kleinsten Quadrate, d.h. durch Minimierung der summierten Quadrate der Residuen
bezüglich a und b.
Nach Ausmultiplikation, Ableiten und Nullsetzen
erhält man die gesuchten Regressionskoeffizienten als die Lösungen
und
-
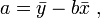 , wobei
, wobei 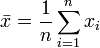 .
.
Mit dem Verschiebungssatz:
Schätzungen ŷ
Residuen ri :
Stichprobenvarianz der Residuen:
Bestimmtheitsmaß
mit dem Verschiebungssatz :
Varianz der Residuen