0/12

13 Differentialrechnung

0/12/2

13.2 Ableitungsregeln

0/12/2/7

13.2.7 Ableitung der Umkehrfunktion

0/12/2/7/0

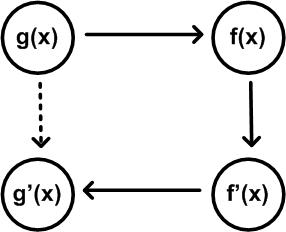
Gegeben sei eine Funktion $y = f (x)$ , von der die Ableitung $y^{'} = f^{'} (x)$ sowie die Umkehrfunktion $y = f^{- 1} (x) = g (x)$ gebildet werden kann. .
Falls die Ableitung der Umkehrfunktion $y^{'} = f^{'} (x)$ nun nicht mit den bisherigen Verfahren gebildet werden kann, läßt sich die Umkehrfunktion $y = f^{- 1} (x) = g (x)$ evtl. doch ableiten:
0/12/2/7/1

Abbildung 1: Ableitung der Umkehrfunktion

0/12/2/7/2 .
Das Prinzip: .

Funktionsgleichung nach x auflösen: $x = f^{- 1} (y) = g (y)$
Anders ausgedrückt: $f (x) = f (g (y)) = f (f^{- 1} (y)) = y$

innere Funkion		$g (y)$	$=$	$u$
äußere Funkion		$f (u)$
Kettenregel:		$\frac{d y}{d y}$	$=$	$\frac{d (f (g (y)))}{d y}$
$1$	$=$	$\frac{d f}{d u} \cdot \frac{d u}{d y}$	$=$	$f^{'} (x) \cdot g^{'} (y)$
	$\Rightarrow$	$g^{'} (y)$	$=$	$\frac{1}{f^{'} (x)}$

.
.
Die Schritte zur Ableitung der Umkehrfunktion

g (x) :

1.: Ersetzen der Variablen $x$ durch $g (y)$ und ableiten
2.: Auf beiden Seiten $x$ und $y$ vertauschen

Beispiel 13 - 1:
Gegeben sei die Umkehrfunktion von $y = e^{x}$ : $x = ln y$ .
sowie die Ableitung von $y = e^{x}$ : $y^{'} = e^{x}$ . .
Gesucht ist die Ableitung $y^{'} = \frac{d ln x}{d x}$ : .
Schritt 1: .
$x = g (y) = ln y$ .
$g^{'} (y) = \frac{1}{f^{'} (x)} = \frac{1}{e^{x}} = \frac{1}{y}$ .
Schritt 2: Vertauschen von $x$ und $y$ :
$g^{'} (x) = \frac{d}{d x} (ln x) = \frac{1}{x}$ .
.
0/12/2/7/3 .
Beispiel 13 - 80

$f (x)$	$=$	$arcsin (x)$	$=$	$y$

$f (x)$	$=$	$arcsin (x)$	$=$	$y$
$g (y)$	$=$	$sin (x)$
${(arcsin x)}^{'}$	$=$	$f^{'} (y)$	$=$	$\frac{1}{g^{'} (x)}$	$=$	$\frac{1}{(sin x^{)}'}$
	$=$	$\frac{d}{d x} arcsin (x)$	$=$	$\frac{1}{\sqrt{1 - x^{2}}}$

.
0/12/2/7/4