0/12

13 Differentialrechnung

0/12/2

13.2 Ableitungsregeln

0/12/2/9

13.2.9 Differential einer Funktion

0/12/2/9/0

0/12/2/9/1

Abbildung 1: Differential

0/12/2/9/2 .

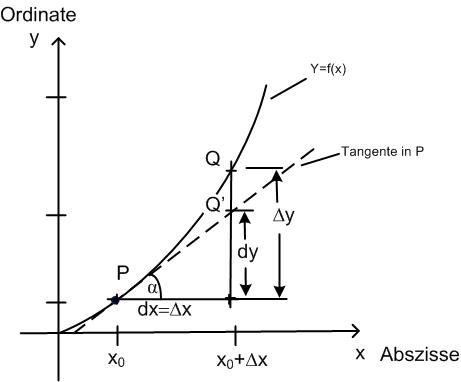
Fragestellung: Wie groß wird der Fehler, wenn anstelle der Tangentensteigung die Sekantensteigung für ein $Δ x$ (z.B. von 0.1) verwendet wird ? .
.
Differential $d y = d f = f^{'} (x_{0}) \cdot$ .
$\to$ Zuwachs der Ordinate der Kurventangente an $x_{0}$
bei Änderung der Abszisse $x$ um $d x$ .
$Δ y - d y$ : Ordinatenabweichung .
Die Ableitung einer Funktion kann als Quotient zweier Differentiale aufgefasst werden. $y^{'} = f^{'} (x) = \frac{d y}{d x} = lim_{Δ x \to 0} \frac{Δ y}{Δ x}$

Beispiel 13 - 1: .
Gesucht ist Steigung der Sekante, also die Ordinatenänderung $Δ y$ für eine Änderung von $Δ x = 0, 1$ an $x = 1$ . .
.

Für $y$	$=$	$x^{2} + e^{x - 1}$	in $P = (\binom{1}{2})$
Für $Δ x$	$=$	$0, 1$
$Δ y$	$=$	$f (x + Δ x) - f (x)$
	$=$	$f (1 + 0, 1) - f (1)$
	$\approx$	$2, 315 - 2 \approx 0, 315$

Damit ist die Steigung der Sekante im Punkt

P = (\binom{1}{2})

ungefähr

3, 15

. .
Steigung der Kurventangente: .

$f^{'} (x)$	$=$	$2 x + e^{x - 1}$
$f^{'} (1)$	$=$	$3$

.
Differenz der Steigungen:

m_{s} - m_{t} \approx 3, 15 - 3 = 0, 15

\to

Der relative Fehler ist dann

F =

Steigungsdifferenz / Steigung

\approx \frac{0, 15}{3} \approx 5 %