0

0/12

13 Differentialrechnung

0/12/3

13.3 Anwendung der Differentialrechnung

0/12/3/2

13.3.2 Charakteristische Kurvenpunkte, Monotonie

1.

Monotonie

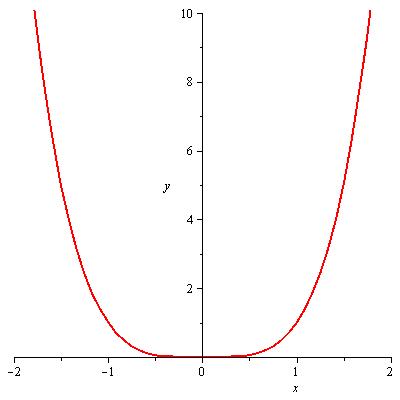
$f^{\prime }\left(x_0\right)>0$	Funktionskurve steigt streng monoton beim Durchgang durch $x_0$
$f^{\prime }\left(x_0\right)\ge 0$	Funktionskurve steigt monoton beim Durchgang durch $x_0$
$f^{\prime }\left(x_0\right)<0$	Funktionskurve fällt streng monoton beim Durchgang durch $x_0$
$f^{\prime }\left(x_0\right)\le 0$	Funktionskurve fällt monoton beim Durchgang durch $x_0$

Beispiel 13 - 1: .

---

.

Abbildung 1: Monotonie

---

.

$y$	$=$	$x^4$
$y^{\prime }$	$=$	$4x^3$	$\left\{\genfrac{}{}{0ex}{}{<0\text{ für }x<0}{>0\text{ für }x>0}\right.$

.

.
Beispiel 13 - 84

$y$	$=$	$x^3+2x$

.

$y$	$=$	$x^3+2x$
$y^{\prime }$	$=$	$3x^2+2$	$>0$

.
.
Beispiel 13 - 85

$y$	$=$	$|x^2-2x+1|$	$\left(x\ge 1\right)$

.

$y$	$=$	$|x^2-2x+1|$	$\left(x\ge 1\right)$
$y$	$=$	$x^2-2x+1$
$y^{\prime }$	$=$	$2x-2$	$>0$

.

2.

2. Ableitung, Krümmung

---

$f^{″}\left(x\right)>0$	$f^{″}\left(x\right)<0$
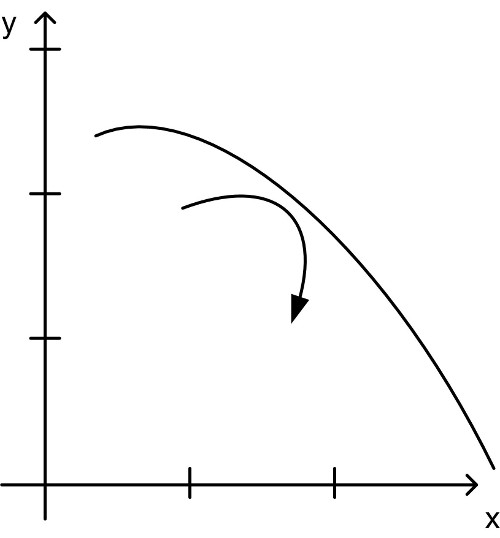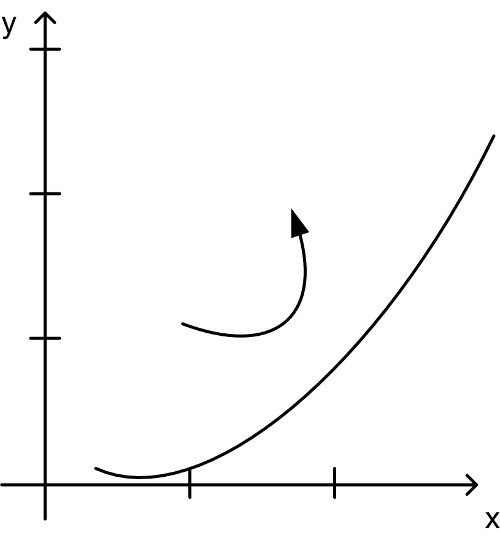
Linkskrümmung	Rechtskrümmung
konvex	konkav

Abbildung 6: Krümmung

---

Krümmung $k=\frac{f^{″}\left(x\right)}{{\left(1+f^{\prime }{\left(x\right)}^2\right)}^{\frac{3}{2}}}$

.
Beispiel 13 - 86
Kreisgleichung, obere Hälfte

$y$	$=$	$\sqrt{r^2-x^2}$	$=$	${\left(r^2-x^2\right)}^{\frac{1}{2}}$

.

$y$	$=$	$\sqrt{r^2-x^2}$	$=$	${\left(r^2-x^2\right)}^{\frac{1}{2}}$
$y^{\prime }$	$=$	$\frac{-2x}{2}\cdot {\left(r^2-x^2\right)}^{-\frac{1}{2}}$	$=$	$-x{\left(r^2-x^2\right)}^{-\frac{1}{2}}$
$y^{″}$	$=$	$-{\left(r^2-x^2\right)}^{-\frac{1}{2}}-\frac{2x^2}{2}\cdot {\left(r^2-x^2\right)}^{-\frac{3}{2}}$
	$=$	$\frac{-1}{{\left(r^2-x^2\right)}^{\frac{1}{2}}}+\frac{-x^2}{{\left(r^2-x^2\right)}^{\frac{3}{2}}}$
	$=$	$\frac{-r^2}{{\left(r^2-x^2\right)}^{\frac{3}{2}}}$

$\Rightarrow$
$\frac{y^{″}}{{\left(1+{\left(y^{\prime }\right)}^2\right)}^{\frac{3}{2}}}$	$=$	$\frac{\frac{-r^2}{{\left(r^2-x^2\right)}^{\frac{3}{2}}}}{{\left(1+\frac{x^2}{\left(r^2-x^2\right)}\right)}^{\frac{3}{2}}}$	$=$	$\frac{\left(\frac{-r^2}{{\left(r^2-x^2\right)}^{\frac{3}{2}}}\right)}{\left({\frac{\left(r^2-x^2\right)+x^2}{\left(r^2-x^2\right)}}^{\frac{3}{2}}\right)}$
	$=$	$\frac{-r^2}{{\left(r^2\right)}^{\frac{3}{2}}}$	$=$	$-\frac{1}{r}$

.
Krümmung $k=-\frac{1}{r}$ (Kehrwert des Radius) .
.
Allgemein gilt: Krümmungsradius $\rho =\frac{1}{\left|k\right|}$