 .
.
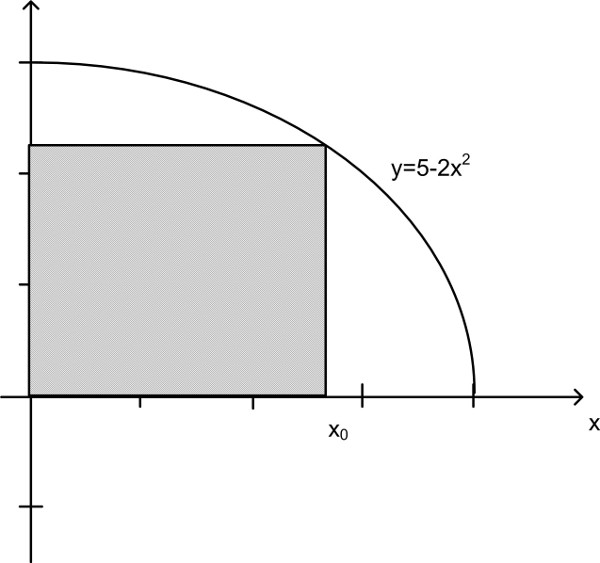
Abbildung 1:
0
0/12
0/12/3
0/12/3/7
0/12/3/7/1 .
Beispiel 13 - 92
Gegeben sei die Funktion .
Ein Rechteck werde durch die x- und y-Achsen sowie einen Punkt der Funktion
begrenzt.
.