 .
.
0
0/12
0/12/3
0/12/3/7
0/12/3/7/5 .
Beispiel 13 - 94
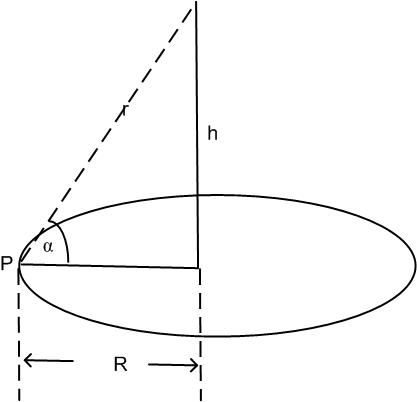
Gegeben ist eine Lampe mit der Lichtstärke .
In Punkt
gilt für die Helligkeit:
gesucht ist die maximale Ausleuchtung des Tischrandes.
Wie hoch muss die Lampe aufgehängt werden?
.
d.h. ist
ein Maximum.