0

0/19

20 Anwendungen

0/19/3

20.3 Vektorielle Darstellung der Ebene

0/19/3/7

20.3.7 Schnittpunkt/Schnittwinkel einer Geraden mit einer Ebene

1.

Die Ebene liegt in Parameterdarstellung vor .
Zu lösen ist dann das Gleichungssystem .
$\vec{E}=\overrightarrow{r_1}+{\lambda }_1\overrightarrow{a_1}+{\lambda }_2\overrightarrow{a_2}=\overrightarrow{r_2}+\mu \vec{b}$ . 

Beispiel 20 - 219
Schnittpunkt Gerade - Ebene bei Darstellung in Punkt-Richtungsform. .
Gegeben sei eine Ebene mit dem Ortsvektor .
$$

$\overrightarrow{r_1}=\left(\begin{array}{c}3\\ 4\\ 1\end{array}\right)$ , den Richtungsvektoren   $\overrightarrow{a_1}=\left(\begin{array}{c}1\\ 2\\ 0\end{array}\right)$ und     $\overrightarrow{a_2}=\left(\begin{array}{c}2\\ -1\\ -5\end{array}\right)$
sowie eine Gerade mit dem Ortsvektor .
$\overrightarrow{r_2}=\left(\begin{array}{c}2\\ 1\\ 5\end{array}\right)$ und dem Richtungsvektor     $\overrightarrow{b}=\left(\begin{array}{c}3\\ -4\\ 0\end{array}\right)$ . .
Bestimmen Sie den Schnittpunkt. .

Zu lösen ist das Gleichungssystem $\left(\begin{array}{c}\hfill 3\hfill \\ \hfill 4\hfill \\ \hfill 1\hfill \\ \hfill \hfill \end{array}\right)+{\lambda }_1\left(\begin{array}{c}\hfill 1\hfill \\ \hfill 2\hfill \\ \hfill 0\hfill \\ \hfill \hfill \end{array}\right)+{\lambda }_2\left(\begin{array}{c}\hfill 2\hfill \\ \hfill -1\hfill \\ \hfill -5\hfill \\ \hfill \hfill \end{array}\right)=\left(\begin{array}{c}\hfill 2\hfill \\ \hfill 1\hfill \\ \hfill 5\hfill \\ \hfill \hfill \end{array}\right)+\mu \left(\begin{array}{c}\hfill 3\hfill \\ \hfill -4\hfill \\ \hfill 0\hfill \\ \hfill \hfill \end{array}\right)$. .

Für x:	${\lambda }_1$	$+2{\lambda }_2$	$-3\mu$	$=$	$-1$
Für y:	$2{\lambda }_1$	$-{\lambda }_2$	$+4\mu$	$=$	$-3$
Für z:		$-5{\lambda }_2$		$=$	$4$

${\lambda }_1$	${\lambda }_2$	$\mu$	$c$
$1$	$2$	$-3$	$-1$
$2$	$-1$	$4$	$-3$	nach III
$0$	$-5$	$0$	$4$	nach II
$1$	$2$	$-3$	$-1$
$0$	$-5$	$0$	$4$	:-5
$2$	$-1$	$4$	$-3$	-2I
$1$	$2$	$-3$	$-1$	-2II
$0$	$1$	$0$	$-\frac{4}{5}$
$0$	$-5$	$10$	$-1$	+5II, :5
$1$	$0$	$-3$	$\frac{-5+8}{5}$	+3III
$0$	$1$	$0$	$-\frac{4}{5}$
$0$	$0$	$1$	$-\frac{1}{2}$
$1$	$0$	$0$	$\frac{6-15}{10}$	-2II
$0$	$1$	$0$	$-\frac{4}{5}$
$0$	$0$	$1$	$-\frac{1}{2}$

.

Lösung: ${\lambda }_1=-\frac{9}{10}$; ${\lambda }_2=-\frac{4}{5}$; $\mu =-\frac{1}{2}$ .
Der Schnittpunkt kann über die Ebenengleichung oder über die Geradengleichung bestimmt werden (dient als Probe !) und liegt bei: .
$\left(\begin{array}{c}\hfill 3\hfill \\ \hfill 4\hfill \\ \hfill 1\hfill \\ \hfill \hfill \end{array}\right)-\frac{9}{10}\left(\begin{array}{c}\hfill 1\hfill \\ \hfill 2\hfill \\ \hfill 0\hfill \\ \hfill \hfill \end{array}\right)-\frac{4}{5}\left(\begin{array}{c}\hfill 2\hfill \\ \hfill -1\hfill \\ \hfill -5\hfill \\ \hfill \hfill \end{array}\right)=\left(\begin{array}{c}\hfill 2\hfill \\ \hfill 1\hfill \\ \hfill 5\hfill \\ \hfill \hfill \end{array}\right)-\frac{1}{2}\left(\begin{array}{c}\hfill 3\hfill \\ \hfill -4\hfill \\ \hfill 0\hfill \\ \hfill \hfill \end{array}\right)=\left(\begin{array}{c}\hfill 3-\frac{9+16}{10}\hfill \\ \hfill 4-\frac{18-8}{10}\hfill \\ \hfill 1+\frac{40}{10}\hfill \\ \hfill \hfill \end{array}\right)=\left(\begin{array}{c}\hfill 3-\frac{5}{2}\hfill \\ \hfill 3\hfill \\ \hfill 1+4\hfill \\ \hfill \hfill \end{array}\right)=\left(\begin{array}{c}\hfill \frac{1}{2}\hfill \\ \hfill 3\hfill \\ \hfill 5\hfill \\ \hfill \hfill \end{array}\right)$. .

.
.

2.

Die Ebene liegt in Normalendarstellung vor

Der Ortsvektor $\overrightarrow{r_s}$ des Schnittpunkts muss sowohl die Geradengleichung als auch die Ebenengleichun erfüllen: .
$\overrightarrow{r_s}=\overrightarrow{r_1}+{\lambda }_s\cdot \vec{a}$ .
$\vec{n}\cdot \left(\overrightarrow{r_s}-\overrightarrow{r_0}\right)=0$. .
Einsetzen der ersten Gleichung in die zweite und Auflösen nach ${\lambda }_S$ ergibt den Wert für den Schnittpunkt: .

.
Beispiel 20 - 220

$\overrightarrow{n}\cdot \left(\overrightarrow{r_1}+{\lambda }_s\overrightarrow{a}-\overrightarrow{r_0}\right)=0$ .
$$

⋅( - )+λs( ⋅ ) = 0 .
${\lambda }_s=\frac{\overrightarrow{n}\cdot \left(\overrightarrow{r_0}-\overrightarrow{r_1}\right)}{\overrightarrow{n}\cdot \overrightarrow{a}}$. .
Oben eingesetzt, erhält man: .
$\overrightarrow{r_s}=\overrightarrow{r_1}+{\lambda }_s\cdot \overrightarrow{a}=\overrightarrow{r_s}=\overrightarrow{r_1}+\frac{\overrightarrow{n}\cdot \left(\overrightarrow{r_0}-\overrightarrow{r_1}\right)}{\overrightarrow{n}\cdot \overrightarrow{a}}\cdot \overrightarrow{a}$ .

---

.

Abbildung 1: Schnittwinkel Gerade - Ebene

---

.
.
Damit ergibt sich: $\overrightarrow{r_s}=\overrightarrow{r_1}+\left(\frac{\vec{n}\cdot \left(\overrightarrow{r_0}-\overrightarrow{r_1}\right)}{\vec{n}\cdot \vec{a}}\right)\cdot \vec{a}$.
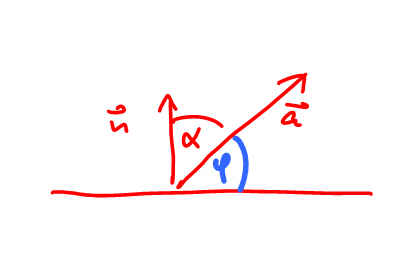
Der Schittwinkel $\phi =90^o-\alpha$ berechnet sich über das Skalarprodukt: .

$cos\left(90^o-\alpha \right)=sin\alpha =\frac{\vec{n}\cdot \vec{a}}{\left|\vec{n}\right|\cdot \left|\vec{a}\right|}$ bzw. $\alpha =arcsin\left(\frac{|\vec{n}\cdot \vec{a}|}{\left|\vec{n}\right|\cdot \left|\vec{a}\right|}\right)$ . .