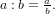Bruchrechnung

Definition: Bruch, Zähler und Nenner

Das Ergebnis einer Division einer beliebigen reellen Zahl durch eine beliebige reelle Zahl ungleich Null, kann als Bruch geschrieben werden, d.h.

a heißt dabei Zähler des Bruches und b heißt dabei Nenner des Bruches.

Anschaulich sagt die Definition lediglich aus, dass der Bruch $\frac{a}{b}$ entsteht, wenn man a Ganze durch b Teile teilt. Alternativ könnte man auch ein Ganzes in b Teile teilen und davon a Stücke nehmen. Beiden Anschauungen führen zum gleichen Ergebnis, wie man an einem einfachen Beispiel leicht sehen kann: So ist es egal, ob Sie von 3 identischen Pizzen jeweils $\frac{1}{4}$ bekommen oder ob Sie von einer in Viertel geteilten Pizza 3 Stücke bekommen. Sie bekommen jeweils $\frac{3}{4}$ Pizzen.

Für Brüche gelten die folgenden Rechengesetze:

Satz: Rechnen mit Brüchen

Seien $a,c \in \mathbb{R}$ und $b,c \in \mathbb{R}\setminus\{0\}$. Dann gilt:

Kürzen und Erweitern: $\frac{a}{b}=\frac{a\cdot x}{b\cdot x}$ für jede beliebige Zahl $x \ne 0$.
Dabei heißt die Umformung von links nach rechts erweitern und die Umformung von rechts nach links kürzen.
Addition und Subtraktion: $\frac{a}{b}\pm \frac{c}{d}=\frac{ad}{bd}\pm \frac{cb}{db}=\frac{ad\pm cb}{bd}$
Achtung bei der Addition bzw. Subtraktion zweier Brüche muss zuerst ein gemeinsamer Hauptnenner bestimmt werden.
Multiplikation: $\frac{a}{b}\cdot \frac{c}{d}=\frac{a\cdot c}{b \cdot d}$
Division: $\frac{a}{b} : \frac{c}{d}=\frac{a}{b}\cdot \frac{d}{c}=\frac{a\cdot d}{b \cdot c}$
Durch einen Bruch wird dividiert indem man mit dem Kehrwert multipliziert.
Doppelbrüche: $\frac{\frac{a}{b}}{\frac{c}{d}}=\frac{a}{b} : \frac{c}{d}$

Beispiel 1. Rechnen mit Brüchen

Vereinfachen Sie den folgenden Ausdruck: \begin{eqnarray*}\frac{\frac{b}{a}:5-\frac{a}{b}:\frac{1}{4}}{3\cdot\frac{a}{b}-\frac{3a-1}{b}}=\end{eqnarray*}

\begin{eqnarray*} &=&\frac{\frac{b}{a}:\color{red}{\frac{5}{1}}-\frac{a}{b}:\frac{1}{4}}{3\cdot\frac{a}{b}-\frac{3a-1}{b}} \quad \end{eqnarray*}

die Zahl 5 wird als Bruch geschrieben um dann die Divisionsregel anwenden zu können

\begin{eqnarray*} &=& \frac{\frac{b}{a}\color{red}{\cdot \frac{1}{5}}-\frac{a}{b}\color{red}{\cdot \frac{4}{1}}}{3\cdot\frac{a}{b}-\frac{3a-1}{b}} \quad & \end{eqnarray*}

Divisionen werden in Multiplikationen verwandelt, indem der Kehrwert des Divisors (Zahl durch die geteilt wird) gebildet wird

\begin{eqnarray*} &=& \frac{\color{red}{\frac{b\cdot 1}{a \cdot 5}}-\color{red}{\frac{a \cdot 4}{b \cdot 1}}}{\color{red}{\frac{3\cdot a}{1 \cdot b}}-\frac{3a-1}{b}} \quad & \end{eqnarray*}

Durchführung der drei Multiplikationen; Achtung: 3 und 4 können als Bruch mit Nenner 1 geschrieben werden

\begin{eqnarray*} &=& \frac{\frac{b}{5a}-\frac{4a}{b}}{\frac{3a}{b}-\frac{3a-1}{b}} \end{eqnarray*}

\begin{eqnarray*} &=& \frac{\frac{b \color{red}{\cdot b}}{5a\color{red}{\cdot b}}-\frac{4a \color{red}{\cdot 5a}}{b \color{red}{\cdot 5a}}}{\frac{3a}{b}-\frac{3a-1}{b}} \quad & \end{eqnarray*}

oberen beiden Brüche erweitert um sie auf einen gemeinsamen Nenner zu bringen

\begin{eqnarray*} &=& \frac{\frac{b\cdot b-4a\cdot 5a}{5ab}}{\frac{3a-\color{red}{(}3a-1\color{red}{)}}{b}} \quad & \end{eqnarray*}

Subtraktion im Zähler und Nenner; Achtung: Klammer muss gesetzt werden

\begin{eqnarray*} &=& \frac{\frac{b^2-20a^2}{5ab}}{\frac{3a\color{red}{-3a+1}}{b}} \quad & \end{eqnarray*}

Vereinfachen und Klammer auflösen

\begin{eqnarray*} &=& \frac{\frac{b^2-20a^2}{5ab}}{\frac{1}{b}} \end{eqnarray*}

\begin{eqnarray*} &=& \frac{b^2-20a^2}{5ab}: \frac{1}{b}\quad & \end{eqnarray*}

Definition eines Bruches als Division verwendet (Doppelbrüche)

\begin{eqnarray*} &=& \frac{b^2-20a^2}{5ab} \cdot \frac{b}{1} & \end{eqnarray*}

Division wird in Multiplikation verwandelt, indem der Kehrwert des Divisors gebildet wird

\begin{eqnarray*} &=& \frac{\color{red}{(}b^2-20a^2\color{red}{)} \cdot b}{5ab \cdot 1} \quad & \end{eqnarray*}

Durchführung der Multiplikation; Achtung: Klammer muss gesetzt werden

\begin{eqnarray*} &=& \frac{b^2-20a^2}{5a} \quad & \end{eqnarray*}

mit b gekürzt