Beipiel: Supremum als Metrik

  
Sei B MathType@MTEF@5@5@+= feaagKart1ev2aqaMTbvLHfij5gC1rhimfMBNvxyNvgaCnwyST3q9b WexLMBbXgBcf2CPn2qVrwzqf2zLnharuavP1wzZbItLDhis9wBH5ga rmWu51MyVXgaruWqVvNCPvMCG4uz3bqee0evGueE0jxyaibaieYlf9 irVeeu0dXdh9vqqj=hEeeu0xXdbba9frFj0=OqFfea0dXdd9vqaq=J frVkFHe9pgea0dXdar=Jb9hs0dXdbPYxe9vr0=vr0=vqpWqaaeaabi GaciaacaqabeaadaqaaqaaaOqaaabaaaaaaaaapeGaam4qaaaa@40AC@  die Menge aller beschränkten Funktionen die auf dem abgeschlossenen Intervalls [a,b] MathType@MTEF@5@5@+= feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9 vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaaeaaaaaaaaa8 qacaGGBbGaaGimaiaacYcacaaIXaGaaiyxaaaa@39FC@   definiert sind. Wir definieren auf  B eine Metrik durch ρ sup ( f 1 , f 2 )=sup{| f 1 ( x )− f 2 ( x ) |:a≤x≤b} MathType@MTEF@5@5@+= feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9 vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaaeaaaaaaaaa8 qacqaHbpGCpaWaaSbaaSqaa8qacaWGZbGaamyDaiaadchaa8aabeaa kmaabmaabaGaamOzamaaBaaaleaapeGaaGymaaWdaeqaaOGaaiilai aadAgadaWgaaWcbaWdbiaaikdaa8aabeaaaOGaayjkaiaawMcaaiab g2da9iGacohacaGG1bGaaiiCaiaacUhadaabdaqaaiaadAgadaWgaa WcbaWdbiaaigdaa8aabeaakmaabmaabaGaamiEaaGaayjkaiaawMca aiabgkHiTiaadAgadaWgaaWcbaWdbiaaikdaa8aabeaakmaabmaaba GaamiEaaGaayjkaiaawMcaaaGaay5bSlaawIa7aiaacQdacaaIWaGa eyizImQaamiEaiabgsMiJkaaigdacaGG9baaaa@5AE9@ Dieses Supremum existiert, da mit f 1 MathType@MTEF@5@5@+= feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9 vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOzamaaBa aaleaaqaaaaaaaaaWdbiaaigdaa8aabeaaaaa@37F8@ und f 2 MathType@MTEF@5@5@+= feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9 vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOzamaaBa aaleaaqaaaaaaaaaWdbiaaigdaa8aabeaaaaa@37F8@  auch | f 1 ( x )− f 2 ( x ) | beschränkt ist (Beweis?).
Übungsaufgabe: Beweisen Sie, dass ρ sup MathType@MTEF@5@5@+= feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9 vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeqyWdi3aaS baaSqaaiGacohacaGG1bGaaiiCaaqabaaaaa@3AC9@ eine Metrik definiert!
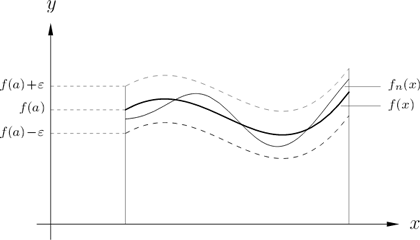
Die ε MathType@MTEF@5@5@+= feaagKart1ev2aqaM9bvLHfij5gC1rhimfMBNvxyNvgaCzxyYvgCZL gBV5gatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1B TfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaG qiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0x bba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adba qaaeGaciGaaiaabeqaamaabaabaaGcbaaeaaaaaaaaa8qacqaH1oqz aaa@4367@ -Umgebung einer Funktion f MathType@MTEF@5@5@+= feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9 vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOzaaaa@36E2@ ist danndie Menge aller Funktionen g MathType@MTEF@5@5@+= feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9 vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4zaaaa@36E3@ , die sich für ein δ∈(0,ε) an jeder Stelle des Intervalls von f MathType@MTEF@5@5@+= feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9 vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOzaaaa@36E2@ um weniger als ε−δ MathType@MTEF@5@5@+= feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9 vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaaeaaaaaaaaa8 qacqaH1oqzcqGHsislcqaH0oazaaa@3A50@ unterscheiden.
Daraus ergibt sich, dass der Begriff der Konvergenz einer Folge ( f n ) MathType@MTEF@5@5@+= feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9 vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcqaaaaaaaaaWdbe aadaqadaqaaiaadAgapaWaaSbaaSqaa8qacaWGUbaapaqabaaak8qa caGLOaGaayzkaaaaaa@39F2@ gegen eine Funktion f MathType@MTEF@5@5@+= feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9 vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcqaaaaaaaaaWdbe aapaGaamOzaaaa@3711@ im metrischen Raum ( B, ρ sup ) MathType@MTEF@5@5@+= feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9 vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcqaaaaaaaaaWdbe aadaqadaqaaiaadkeacaGGSaGaeqyWdi3aaSbaaSqaaiGacohacaGG 1bGaaiiCaaqabaaakiaawIcacaGLPaaaaaa@3DF3@ mit dem Begriff der gleichmäßigen Konvergenz übereinstimmt.