Im ebenen,
rechtwinkligen Dreieck gelten (bezogen auf die
Benennungen in der oberen Zeichnung):
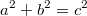 Als
Satz formuliert:
Als
Satz formuliert: Die Summe der Flächeninhalte
der Quadrate über den Katheten entspricht dem
Flächeninhalt des Quadrats über der Hypotenuse.
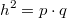 Als
Satz formuliert:
Als
Satz formuliert: Der Flächeninhalt des
Quadrats über der Höhe entspricht dem Flächeninhalt
des Rechtecks, dessen Seiten die Hypotenusenabschnitte
sind.
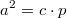
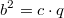 Als
Satz formuliert:
Als
Satz formuliert: Der Flächeninhalt des
Quadrats über einer Kathete entspricht dem
Flächeninhalt des Rechtecks, dessen Seiten die
Hypotenuse und der zur Kathete gehörende
Hypotenusenabschnitt sind.
 Bemerkung
1:
Bemerkung
1: Die bekannte Formel
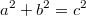
alleine ist
nicht der Satz
des Pythagoras! Durch die Formel alleine ist nämlich
nicht festgelegt, welche Größen

,

und

bezeichnen (

und

müssen ja nicht automatisch die Katheten sein) bzw. ob
es sich bei

,

und

überhaupt um Seiten
eines rechtwinkligen Dreiecks handelt. Für
irgendwelche beliebigen

,

und

wäre es denn auch eher
überraschend, wenn sie die Beziehung
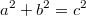
erfüllen würden. Warum
sollten sie...
Bemerkung
2: Der Satz des Pythagoras gilt natürlich
auch in den beiden Teildreiecken, die sich in der
Skizze ergeben, da die Höhe und die Hypotenuse einen
rechten Winkel einschließen. Hierbei liegen die Seiten

bzw.

(vormals die Katheten)
gegenüber des rechten Winkels. In den Teildreiecken
ist also

bzw.

die
Hypotenuse.
Es gilt also:
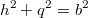
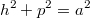 Bemerkung
3:
Bemerkung
3: Bei konkreten Berechnungen müssen diese
Formeln, die ja letztendlich
quadratische
Gleichungen sind, teilweise umgeformt werden, z.
B. um
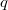
aus
dem Höhensatz berechnen zu können.
 Brückenkurs
Brückenkurs