Ein Koordinatensystem ist ein geometrisches Schema, welches benutzt wird, um Punkte, Funktionsgraphen etc. eindeutig zu positionieren. In diesem Lernmodul werden nur Koordinatensysteme, bei denen die Achsen im rechten Winkel zueinander stehen, verwendet. Man nennt sie auch kartesische Koordinatensysteme - nach dem französischen Philosoph und Mathematiker René Descartes, der sich als einer der ersten intensiv mit ihnen beschäftigt hat und damit für ihre Verbreitung gesorgt hat.

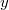
Für zwei Dimensionen (sprich: für die Ebene) braucht man naheliegenderweise zwei Achsen. Die horizontale Achse nennen wir in einem solchen Fall Abszisse, die vertikale Achse Ordinate. Heißen die Variablen und , sagt man statt Abszisse auch x-Achse und statt Ordinate auch y-Achse; bei anderen Variablenbezeichnungen entsprechend. Die Achsen sollten immer beschriftet werden. Wenn es sich anbietet, kann dazu der inhaltliche Zusammenhang einschließlich der entsprechenden Einheit verwendet werden, z. B. "Zeit in Stunden". Um die Darstellung im Koordinatensystem nicht zu verzerren, ist es meist hilfreich, auf beiden Achsen die gleiche Skaleneinteilung zu verwenden. Um das Koordinatensystem vollständig zu machen, bekommen die Achsen an ihrem positiven Ende einen kleinen Pfeil, der andeutet, dass auch größere Zahlenwerte betrachtet werden könnten.

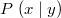
Jeder Punkt in diesem Koordinatensystem hat eine eindeutige "Adresse", die aus zwei Koordinaten besteht: einer x-Koordinate und einer y-Koordinate. Man schreibt dafür . Wichtig dabei ist die Reihenfolge: Der erste Werte bezieht sich immer auf die x-Achse und gibt an, wie weit links oder rechts sich der Punkt befindet. Der zweite Wert bezieht sich immer auf die y-Achse und gibt an, wie weit oben oder unten sich der Punkt befindet. 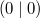Der Punkt heißt Koordinatenursprung oder kurz Ursprung.
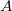
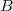
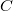
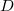
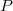
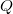
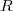
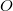
Punkte werden klassischerweise mit großen lateinischen Buchstaben, am liebsten mit , , und oder , und , bezeichnet. Für den Koordinatenursprung hat sich der Buchstabe , vom lateinischen Wort origo für Ursprung, eingebürgert.

Schauen wir uns ein paar Punkte im Koordinatensystem an:






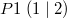
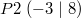
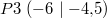
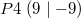
Das obere rechte Viertel des Koordinatensystems heißt 1. Quadrant. Hier sind sowohl x- als auch y-Werte positiv.
Das obere linke Viertel des Koordinatensystems heißt 2. Quadrant. Hier sind die x-Werte negativ und die y-Werte positiv.
Das untere linke Viertel des Koordinatensystems heißt 3. Quadrant. Hier sind sowohl x- als auch y-Werte negativ.
Das untere rechte Viertel des Koordinatensystems heißt 4. Quadrant. Hier sind die x-Werte positiv und die y-Werte negativ.

Bitte wundern Sie sich nicht über die Reihenfolge der Nummerierung. Drehungen entgegengesetzt des Uhrzeigersinns sind in der Mathematik die Regel und werden auch als "mathematisch positiv" bezeichnet. Warum man oben rechts angefangen hat zu zählen, ist vermutlich klar ;-).