Mengen u. a.VorabIst eine Zahl  größer als 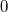 , also 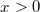 , nennt man sie positiv. Ist eine Zahl  größer oder gleich 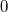 , also 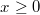 , nennt man sie nichtnegativ. Ist eine Zahl  kleiner als 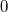 , also 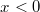 , nennt man sie negativ. Wichtig: 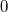 ist weder eine positive noch eine negative Zahl. Mengen, Zahlenbereiche und IntervalleMengenDefinition: Eine Menge ist eine Zusammenfassung von wohlunterschiedenen Objekten, deren Reihenfolge nicht von Belang ist. Es muss aber entscheidbar sein, ob ein Element zu der Menge gehört oder nicht. Mengen können entweder über eine Aufzählung von Elementen (siehe Mengen 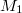 und 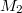 ) oder über eine erklärende Eigenschaft (siehe Menge 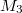 ) definiert werden. Mengen können endlich viele (siehe Menge 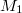 ) oder unendlich viele (siehe Mengen 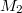 und 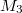 ) Elemente enthalten. Zur Notation: Mengen werden üblicherweise mit großen lateinischen Buchstaben bezeichnet, besonders 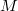 wird (naheliegenderweise) gerne verwendet. Hat man mehrere Mengen, die 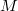 heißen sollen, kann man für die Unterscheidung einen so genannten Index (Plural: Indizes), also eine kleine, tiefgestellte Zahl, verwenden. Für die Angabe der Elemente verwendet man geschweifte Klammern, z. B. -
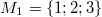 bedeutet: Die Menge, die die Elemente bedeutet: Die Menge, die die Elemente 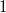 , , 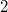 und und 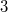 enthält. enthält.
-
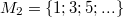 bedeutet: Die Menge aller positiven, ungeraden Zahlen bedeutet: Die Menge aller positiven, ungeraden Zahlen
-
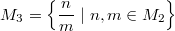 bedeutet: Die Menge aller Brüche mit der Eigenschaft, dass Zähler und Nenner Elemente der oben definierten Menge bedeutet: Die Menge aller Brüche mit der Eigenschaft, dass Zähler und Nenner Elemente der oben definierten Menge 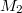 sind. Z. B. sind sind. Z. B. sind  und und 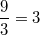 in dieser Menge enthalten. in dieser Menge enthalten.
Bemerkung 1: Um Missverständnissen vorzubeugen, sollten Zahlen in einer Menge mit Semikolons getrennt werden. Sonst könnte 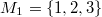 sowohl 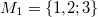 als auch 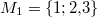 oder 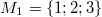 bedeuten - und solche Mehrdeutigkeiten sind bei der Verständigung z. B. über Lösungswege sehr hinderlich und auch grundsätzlich in der Mathematik äußerst unbeliebt... Bemerkung 2: Üblich ist, die Elemente der Größe nach zu sortieren. Wenn Variablen enthalten sind, werden diese alphabetisch sortiert. Dies hat keine mathematischen Hintergründe, verhindert aber, dass man den Überblick verliert. Nun noch ein paar Begriffe, die wir später brauchen werden: Die Schnittmenge 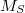 zweier gegebener Mengen 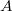 und 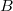 umfasst alle Elemente, die sowohl in 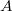 als auch in 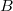 enthalten sind. Anders formuliert: Alle Elemente der Schnittmenge müssen in 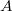 und und in 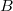 liegen. Mengen, deren Schnittmenge leer ist, nennt man disjunkt. Dann haben die Mengen keine gemeinsamen Elemente. Beispiel: Nehmen wir 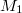 und 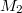 von oben. Nur die Elemente 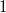 und 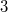 sind in beiden Mengen enthalten, also besteht daraus ihre Schnittmenge. Mathematisch schreibt man das: 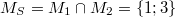 Die Vereinigungsmenge 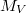 zweier gegebener Mengen 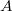 und 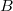 umfasst alle Elemente, die in 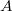 oder in 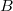 enthalten sind. Beispiel: Wir schauen wieder 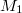 und 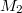 von oben an. Um die Vereinigungsmenge zu bestimmen, nehmen wir erst mal alle Elemente, die in 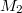 enthalten sind (das sind schließlich mehr). Hinzukommt die 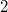 aus der Menge 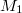 . Um die 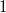 und die 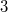 aus 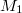 brauchen wir uns nicht mehr zu kümmern, weil sie ja sowieso schon in 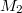 enthalten sind. Mathematisch schreibt man das: 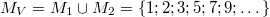 Eine Menge 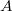 heißt Teilmenge der Menge 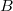 , wenn alle Elemente von 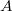 auch in 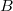 enthalten sind. Beispiel: 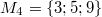 ist eine Teilmenge von 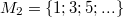 , weil 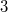 , 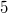 und 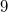 positive, ungerade Zahlen sind. Mathematisch schreibt man hier: 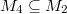 . Um genau zu sein, handelt es sich sogar um eine echte Teilmenge, da in 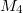 nicht alle Elemente aus 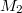 enthalten sind, z. B. ist die 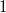 ein Element von 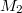 , aber nicht von 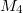 . Auch hierfür gibt es (natürlich) eine mathematische Schreibweise:  . Wenn man einfach von einer Teilmenge (ohne "echt") spricht, können die Mengen also auch gleich sein. Das deutet man bei 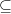 durch den Strich unter dem Bogen an, der an ein Gleichheitszeichen erinnern soll. ZahlenbereicheEinige Mengen sind in der Mathematik so wichtig, dass sie eigene Symbole (Doppelstrich in der Mengenbezeichnung) bekommen haben, z.B. die verschiedenen Zahlenbereiche: 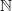 : Menge der natürlichen Zahlen, also 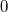 , 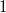 , 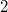 ,  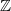 : Menge der ganzen Zahlen, also  , 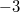 , 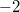 , 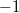 , 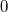 , 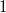 , 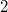 , 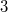 ,  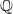 : Menge der rationalen Zahlen, also alle Zahlen, die sich als endlicher oder periodischer Bruch darstellen lassen, mathematisch formuliert: 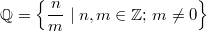 , z.B. 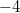 , 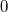 , 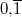 , 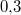 ,  ,  , 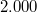 ,  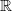 : Menge der reellen Zahlen. Zusätzlich zu den rationalen Zahlen sind hier alle unendlichen, nichtperiodischen Dezimalbrüche enthalten, z.B. 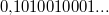 , 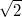 , ![\sqrt [3]{5}](./teximg/img3219.png) , 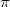 ,  Diese Zahlenbereiche sind so gestaltet, dass sie jeweils Teilmengen voneinander sind: Die natürlichen Zahlen sind eine Teilmenge der ganzen Zahlen, die ganzen Zahlen eine Teilmenge der rationalen Zahlen und die rationalen Zahlen eine Teilmenge der reellen Zahlen. Warum ist das so? Da in den reellen Zahlen alle Brüche (und noch viele Zahlen mehr) enthalten sind, sind natürlich auch die periodischen und endlichen dabei, sprich die rationalen Zahlen. Bastelt man in den rationalen Zahlen einen Bruch mit dem Nenner 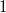 , also z. B. 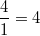 , landet man bei einer ganzen Zahl. Jede nichtnegative, ganze Zahl ist gleichzeitig eine natürliche Zahl. Wer möchte, kann das mathematisch so formulieren: 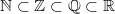 Für den besseren Überblick werden Variablen - aus der Menge der natürlich oder ganzen Zahlen meist
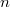 oder oder  , , - aus der Menge der rationalen Zahlen meist
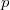 oder oder 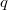 sowie sowie - aus der Menge der reellen Zahlen meist
 , , 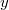 oder oder 
genannt. Es ist natürlich nicht verpflichtend, Variablen so zu benennen - manchmal geht es auch gar nicht... Diese Namenskonventionen haben sich nur eingebürgert, weil sie die Zuordnung der Variablen zu den Zahlenbereichen erleichtern. Zur Notation: Im Zusammenhang mit den Zahlenbereichen werden häufig weitere Symbole und Schreibweisen verwendet, u. a. - Ein hinter dem Zahlenbereichssymbol hochgestelltes
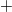 bedeutet, dass nur der positive Teil dieses Zahlenbereichs gemeint ist ( bedeutet, dass nur der positive Teil dieses Zahlenbereichs gemeint ist (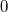 nicht eingeschlossen), z. B. meint nicht eingeschlossen), z. B. meint 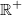 (gesprochen: R plus) die Menge aller reellen Zahlen, die größer als (gesprochen: R plus) die Menge aller reellen Zahlen, die größer als 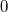 sind. sind.
- Ein hinter dem Zahlenbereichssymbol hochgestelltes
 bedeutet, dass nur der negative Teil dieses Zahlenbereichs gemeint ist ( bedeutet, dass nur der negative Teil dieses Zahlenbereichs gemeint ist (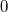 nicht eingeschlossen), z. B. meint nicht eingeschlossen), z. B. meint 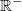 (gesprochen: R minus) die Menge aller reellen Zahlen, die kleiner als (gesprochen: R minus) die Menge aller reellen Zahlen, die kleiner als 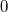 sind. sind.
- Eine hinter dem Zahlenbereichssymbol tiefgestellte
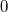 bedeutet, dass die bedeutet, dass die 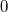 in den Zahlenbereich eingeschlossen wird, z. B. meint in den Zahlenbereich eingeschlossen wird, z. B. meint 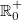 (gesprochen: R null plus) die Menge aller reellen Zahlen, die größer oder gleich (gesprochen: R null plus) die Menge aller reellen Zahlen, die größer oder gleich 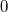 sind. Das ist natürlich nur dann nötig, wenn die sind. Das ist natürlich nur dann nötig, wenn die 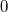 ansonsten nicht in dem Zahlenbereich enthalten wäre. ansonsten nicht in dem Zahlenbereich enthalten wäre.
- Möchte man einzelne Zahlen oder Intervalle aus einem Zahlenbereich ausschließen, verwendet man \ , z. B. meint
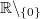 (gesprochen: R ohne null) die Menge der reellen Zahlen ohne die Zahl (gesprochen: R ohne null) die Menge der reellen Zahlen ohne die Zahl 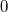 . .
- Möchte man aussagen, dass ein einzelner Wert Teil eines Zahlenbereichs ist oder sein soll, verwendet man
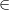 , z. B. meint , z. B. meint 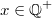 (gesprochen: (gesprochen:  ist Element der positiven rationalen Zahlen), dass ist Element der positiven rationalen Zahlen), dass  eine positive rationale Zahl ist oder sein soll. eine positive rationale Zahl ist oder sein soll.
- Möchte man aussagen, dass ein einzelner Wert nicht Teil eines Zahlenbereichs ist oder sein soll, verwendet man
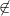 , z. B. meint , z. B. meint 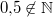 (gesprochen: (gesprochen: 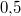 ist nicht Element der natürlichen Zahlen) dass ist nicht Element der natürlichen Zahlen) dass 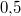 kein Element der natürlichen Zahlen ist. kein Element der natürlichen Zahlen ist.
- Das Symbol
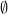 bezeichnet die leere Menge, also die Menge, die keine Elemente enthält. bezeichnet die leere Menge, also die Menge, die keine Elemente enthält.
Bemerkung: Manchmal werden auch andere (ähnliche) Symbole verwendet. Es sollte dann zu Beginn des Artikels erklärt sein, welches Symbol für welchen Zusammenhang verwendet wird. IntervalleDefinition: Ein Intervall ist die Menge aller reellen Zahlen, die zwischen zwei gegebenen Zahlen  und  mit 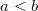 liegen. 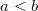 bedeutet nur, dass der untere Rand kleiner sein muss als der obere. Anders gesagt: Ein Intervall ist eine Menge von reellen Zahlen ohne Lücken. Man unterscheidet offene, halboffene und abgeschlossene Intervalle: Bei offenen Intervallen sind die Randwerte nicht im Intervall enthalten. Abgeschlossene Intervalle umfassen auch die Randwerte. Halboffene Intervalle beinhalten einen der beiden Randwerte. Zur Notation: Man verwendet für die Darstellung von Intervallen eckige Klammern. Nach innen gerichtete Klammern schließen den Randwert in das Intervall ein. Nach außen gerichtete Klammern schließen den Randwert aus. Da 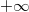 (also "plus unendlich") und 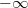 (also "minus unendlich") keine (reellen) Zahlen sind, werden hier immer nach außen gerichtete Klammern bzw. das  - und  -Zeichen verwendet (nicht  und  ) verwendet, z. B. - Das abgeschlossene Intervall
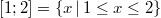 ist die Menge aller reellen Zahlen, die größer oder gleich ist die Menge aller reellen Zahlen, die größer oder gleich 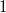 und kleiner oder gleich und kleiner oder gleich 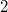 sind. sind.
- Das halboffene Intervall
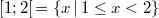 ist die Menge aller reellen Zahlen, die größer oder gleich ist die Menge aller reellen Zahlen, die größer oder gleich 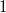 und kleiner, aber nicht gleich und kleiner, aber nicht gleich 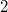 sind. sind.
- Das halboffene Intervall
![]1;2] = \{x \, \vert \, 1 < x \leq 2\}](./teximg/img3252.png) ist die Menge aller reellen Zahlen, die größer, aber nicht gleich ist die Menge aller reellen Zahlen, die größer, aber nicht gleich 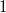 und kleiner oder gleich und kleiner oder gleich 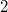 sind. sind.
- Das offene Intervall
![]1;2[ \, = \{x \, \vert \, 1 < x < 2\}](./teximg/img3253.png) ist die Menge aller reellen Zahlen, die größer, aber nicht gleich ist die Menge aller reellen Zahlen, die größer, aber nicht gleich 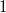 und kleiner, aber nicht gleich und kleiner, aber nicht gleich 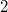 sind. sind.
- Das halboffene Intervall
![]-\infty;2] = \{x \, \vert \, -\infty < x \leq 2\}](./teximg/img3254.png) ist die Menge aller reellen Zahlen, die größer ist die Menge aller reellen Zahlen, die größer 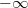 und kleiner oder gleich und kleiner oder gleich 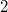 sind. Man benötigt diese Schreibweise z.B., wenn man mithilfe eines Intervalls alle Zahlen beschreiben möchte, die kleiner oder gleich sind. Man benötigt diese Schreibweise z.B., wenn man mithilfe eines Intervalls alle Zahlen beschreiben möchte, die kleiner oder gleich 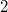 sind, da das Intervall ja auch eine untere Grenze braucht, nicht nur eine obere. sind, da das Intervall ja auch eine untere Grenze braucht, nicht nur eine obere.
-
![[5;2]](./teximg/img3255.png) geht nicht geht nicht
Bemerkung 1: Intervalle lassen sich auch in Mengenschreibweise darstellen. Deswegen wurden gerade auch die ganzen geschweiften Klammern verwendet, z. B. beschreiben die folgenden drei Ausdrücke alle die gleiche Zahlenmenge: 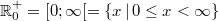 Bemerkung 2: Bemerkung 2: Auch bei Intervallen können das 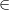 -und das 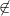 -Zeichen verwendet werden, z.B. gelten 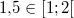 und 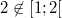 n-TupelDefinition: Ein n-Tupel ist eine geordnete Liste von 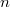 Zahlen. Geordnet bedeutet, dass (anders als bei Mengen) die Reihenfolge, in der die Zahlen notiert sind, wichtig ist. 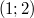 bedeutet also etwas Anderes als 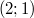 . Deswegen darf man hier natürlich auch nicht der Größe nach sortieren, wie es für Mengen empfohlen wurde. Statt 2-Tupel sagt man Paar und statt 3-Tupel Tripel. Kartesisches Produkt von Mengen: Möchte man die Zahlenbereiche festlegen, aus denen die einzelnen Komponenten eines n-Tupels stammen sollen, so notiert man die entsprechenden Zahlenbereichssymbole mit einem  dazwischen. Soll beispielsweise die erste Komponente eines Zahlenpaars ein Element der reellen Zahlen und die zweite Komponente ein Element der positiven reellen Zahlen sein, schreibt man 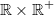 Zur Notation: Zur Notation: Man verwendet für die Darstellung von n-Tupeln runde Klammern, z. B. -
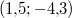 ist ein Zahlenpaar, dessen erste Komponente ist ein Zahlenpaar, dessen erste Komponente 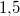 und dessen zweite Komponente und dessen zweite Komponente 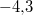 ist. Mit dieser Angabe könnte z. B. ein Punkt in einem 2-dimensionalen Koordinatensystem beschrieben sein. ist. Mit dieser Angabe könnte z. B. ein Punkt in einem 2-dimensionalen Koordinatensystem beschrieben sein.
-
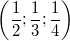 ist ein Zahlentripel, dessen erste Komponente ist ein Zahlentripel, dessen erste Komponente  , dessen zweite Komponente , dessen zweite Komponente  und dessen dritte Komponente und dessen dritte Komponente 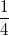 ist. ist.
-
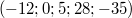 ist ein 5-Tupel, dessen erste Komponente ist ein 5-Tupel, dessen erste Komponente 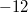 , dessen zweite Komponente , dessen zweite Komponente 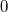 , dessen dritte Komponente , dessen dritte Komponente 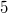 , dessen vierte Komponente , dessen vierte Komponente 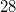 und dessen fünfte Komponente und dessen fünfte Komponente 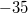 ist. ist.
Definitions- und Wertebereich sowie LösungsmengeSchon mal ein kleiner Vorgriff: Zu Funktionen und Gleichungen (die u.a. in den Kapiteln 5, 6, 9 und 10 behandelt werden) gehört stets die Angabe eines Definitionsbereichs (Formelzeichen: 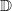 ). Dieser gibt an, welche Zahlen grundsätzlich als Lösung infrage kommen. Insbesondere wenn die Aufgaben in einem inhaltlichen Zusammenhang stehen, sind häufig nur Lösungen aus einem bestimmten Zahlenbereich zugelassen: Ist beispielsweise 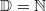 , kann es nur Lösungen aus dem Bereich der natürlichen Zahlen geben. Das ist inhaltlich z.B. dann sinnvoll, wenn eine Anzahl berechnet werden soll (Ein Ergebnis wie " 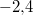 Stück" dürfte selten zu begründen sein...). Auch aus formalen Gründen kann es notwendig sein, den Definitionsbereich einzuschränken: Ist z.B. in einer Gleichung ein Bruch enthalten, muss dafür gesorgt werden, dass der Nenner nie 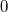 wird. Ist kein Definitionsbereich angegeben und sprechen keine inhaltlichen bzw. formalen Gründe dagegen, kann man davon ausgehen, dass der Definitionsbereich die Menge der reellen Zahlen ist, also 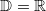 Der Wertebereich (Formelzeichen: 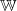 ) einer Funktion ist die Menge aller Funktionswerte, also die Menge der y-Werte. Die Menge aller Lösungen einer Gleichung oder eines Gleichungssystems heißt Lösungsmenge (Formelzeichen:  ).
|
 Brückenkurs
Brückenkurs