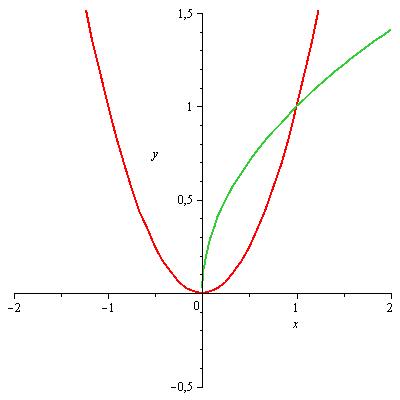
| Abbildung 7: Umkehrfunktion |
Eine Funktion f(x) ist umkehrbar, wenn aus x1≠ x2 stets f(x1)≠ f(x2) folgt.
Bestimmung der Umkehrfunktion :
.
Beispiel 3 - 4
rf9003 .
| y | = | 2x + 1 | |
.
.
Lösung ansehen .
.
.
Beispiel 3 - 5
rf9004 .
| y | = | x2 | |
.
.
Lösung ansehen .
.
Einschränkung des ⅅefinitionsbereichs auf ℝ+ oder ℝ− macht f(x)=x2 umkehrbar, denn dann ergibt sich durch Vertauschen der Variablen
y=√x.

Abbildung 7: Umkehrfunktion
Wichtig:
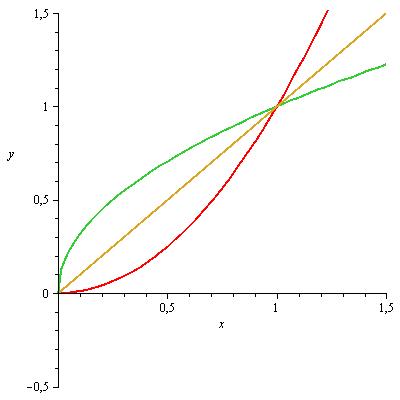
Abbildung 8: Spiegelung an der Winkelhalbierenden