
| Abbildung 9: Polarkoordinaten |

Abbildung 9: Polarkoordinaten
| Abstandskoordinate | r |
| Winkelkoordinate | ϕ |
Umrechnung zwischen Polarkoordinaten
x = r·cosϕ .
y = r·sinϕ .
r = √x2+y2 .
tanϕ = y/x .
.
Beispiel 3 - 8
rf9028 .
Zahlenbeispiel .
Wie lautet die Polarkoordinatendarstellung des Punkts P1 = (2,−5) ?
.
.
Lösung ansehen .
.
.
Beispiel 3 - 9
rf9029 .
Zahlenbeispiel .
Gegeben ist ein Punkt P2 mit r= 5 und ϕ = 5 π/4
Wie lautet die Darstellung des Punkts in kartesischen Koordinaten ?
.
.
Lösung ansehen .
.
.
Beispiel 3 - 10
rf9007 .
Archimedische Spirale .
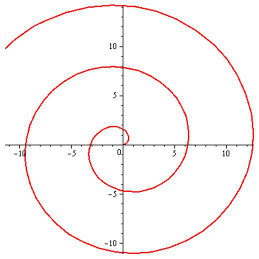
Abbildung 10: Archimedische Spirale
r(ϕ) = 2·ϕ
| ϕ | 0 | π/6 | 2π/6 | 3π/6 | 4π/6 | 5π/6 | π |
.
Darstellung: .
| r | = | 2ϕ ist umkehrbar. | ||
| x | = | r ·cosϕ | = | 2ϕ·cosϕ |
| y | = | r ·sinϕ | = | 2ϕ·sinϕ |
→ Nach Elimination von ϕ ist die Funktion nicht mehr umkehrbar !
.
.
Lösung ansehen .
.