7.2.1  Interpolationspolynome nach Newton

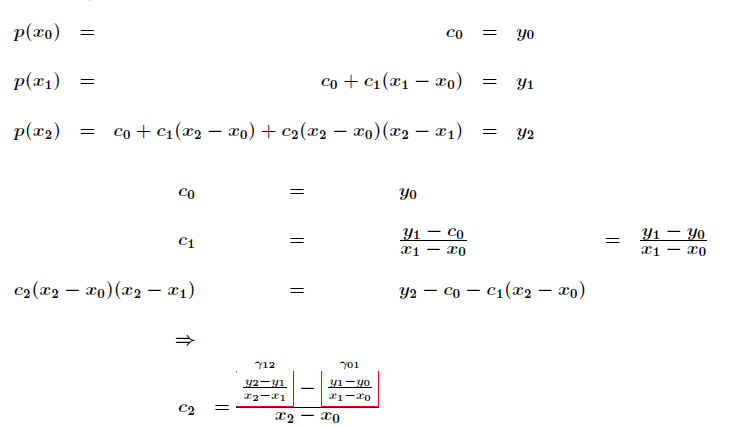
Fragestellung: n-Messpaare liegen vor. Gesucht ist nun ein Interpolationspolynom , das die Werte möglichst exakt beschreibt.

1. Möglichkeit

-

Bei vielen Messwerten wird das Ermitteln der Koeffizienten aufwendig. Besser ist dann das Arbeiten mit Linearfaktoren. Dies leistet das Verfahren der Polynom-Interpolation nach Newton

y=c₀ + c₁(x−x₀)+c₂(x−x₀)(x−x₁) + …+ c_n(x−x₀)(x−x₁) …(x−x_n)


gegeben: Wertepaare (x₀;y₀)(x₁;y₁)…(x_n;y_n)

1. Betrachtung von nur (x₀;y₀)
   ⇒ Es reicht das Polynom von Grad 0
   p₀(x) = c₀=y₀
2. Hinzunehmen von Punkt (x₁;y₁)
   p₁(x) = c₀ + c₁(x−x₀)
   
3. Hinzunehmen von Punkt (x₂;y₂)
   p₂(x) = c₀ + c₁(x−x₀) + c₂(x−x₀)(x−x₁)
   
4. n-Stützstellen
   p(x) = c₀ + c₁(x−x₀)+c₂(x−x₀)(x−x₁) + …+ c_n(x−x₀)(x−x₁) …(x−x_n)
   =∑_i=0ⁿc_i∏_j=0ⁱ⁻¹(x−x_j)
   

Bestimmung der Koeffizienten

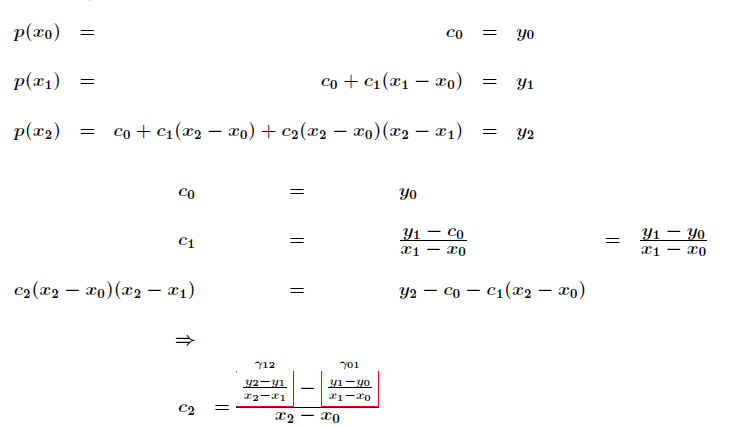
Rekursionsformel:

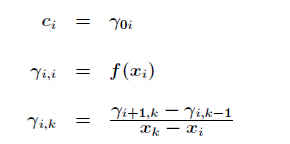
Beispiel 7 - 26:

Rechenschema:

Beispiel 7 - 27 rf9023

.
.
Lösung ansehen .
.