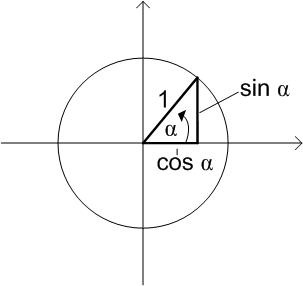
| Abbildung 27: Einheitskreis |
| sin(α + n · 2 π) | = | sinα |
| sin(−α) | = | −sinα |
| cos(α + n · 2π) | = | cosα |
| cos(−α) | = | cosα |
| cos(α) | = | sin(α+π/2) |
| sin(α) | = | cos(α−π/2) |

Abbildung 27: Einheitskreis
| cos2α + sin2α = 1 |
Additionstheoreme
| sin(x1± x2) | = | sinx1 · cosx2 ± cosx1 · sinx2 |
| cos(x1± x2) | = | cosx1 · cosx2 ∓ sinx1 · sinx2 |
| tan(x1± x2) | = | (tanx1 ±tanx2)/ (1∓tanx1 · tanx2) |
| Beispiel 11 - 14: | ||
| sin2α | = | 2·sinα·cosα |
| cos2α | = | cos2α−sin2α |
| 1/2[1−cos(2α)] | = | 1/2[1−cos2α+sin2α] |
| = | 1/2[sin2α+sin2α] | |
| = | sin2α | |
ebenso: .
sin2 α =1/2(1−cos2 α ) .
cos2 α=1/2(1+cos2 α ) .
cos2 α = 2 cos2 α − 1 = 1 − 2 sin2 α = cos2 α − sin2 α