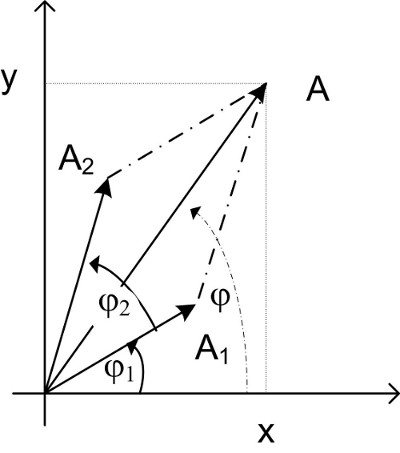
| Abbildung 31: Paralellogramm |
Zwei Schwingungen mit gleicher Frequenz, aber ggf. unterschiedlicher Amplitude und Phase können als eine Schwingung y=y1 + y2 = a · sin(ω t + ϕ) zusammengefasst werden: .
| y1 | = | A1· sin(ω t + ϕ1) |
| y2 | = | A2· sin(ω t + ϕ2) |

Abbildung 31: Paralellogramm
Beispiel 11 - 17 tf9024
| y | = | y1 + y2 |
| zur Vereinfachung: ω t | = | 0 |
| x1 | = | A1· cos(ϕ1) |
| y1 | = | A1· sin(ϕ1) |
| x2 | = | A2· cos(ϕ2) |
| y2 | = | A2· sin(ϕ2) |
| ⇒ | ||
.
.
Lösung ansehen .
.
Beispiel 11 - 18 tf9011
Stellen Sie die Harmonischen Schwingungen
y1= 3 · cos( ω t − π/4) und
y2= −3 · sin( ω t − π/6) durch eine Sinusfunktion vom Typ
y= A · sin( ω t + φ) dar. .
.
Lösung ansehen .
.
Anwendung:
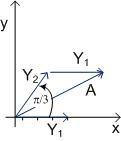
Abbildung 32: Überlagerung von Schwingungen
Beispiel 11 - 19 tf9012
| y1 | = | 4cm · sin(2s−1· t) |
| y2 | = | 3cm · cos(2s−1· t−π/6) |
.
.
Lösung ansehen .
.