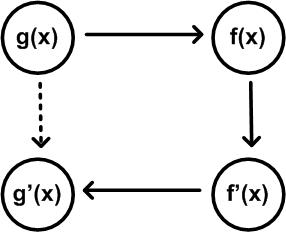
13.2.7  Ableitung der Umkehrfunktion

Gegeben sei eine Funktion y = f(x), von der die Ableitung y′ = f′(x) sowie die Umkehrfunktion y=f⁻¹(x)=g(x) gebildet werden kann. .
Falls die Ableitung der Umkehrfunktion y′ = f′(x) nun nicht mit den bisherigen Verfahren gebildet werden kann, läßt sich die Umkehrfunktion y=f⁻¹(x)=g(x) evtl. doch ableiten:

---

Abbildung 48: Ableitung der Umkehrfunktion

---

.
Das Prinzip: .
.
.
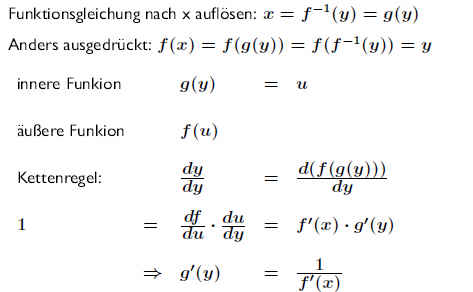Die Schritte zur Ableitung der Umkehrfunktion g(x):

1. Ersetzen der Variablen x durch g(y) und ableiten
2. Auf beiden Seiten x und y vertauschen

Beispiel 13 - 11:
Gegeben sei die Umkehrfunktion von y=e^x: x=lny .
sowie die Ableitung von y=e^x: y′=e^x . .
.
.
Beispiel 13 - 12 df9009

.
.

Lösung ansehen .
.