13.2.9 Differential einer Funktion
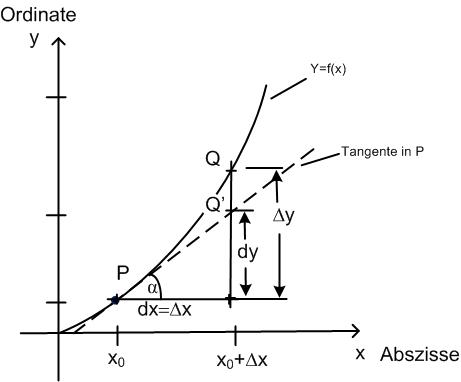
| Abbildung 49: Differential |
Fragestellung: Wie groß wird der Fehler, wenn anstelle der Tangentensteigung die Sekantensteigung für ein Δ x (z.B. von 0.1) verwendet wird ?
Differential dy=df=f′(x0)·
→ Zuwachs der Ordinate der Kurventangente an x0
bei Änderung der Abszisse x um dx
Δ y − dy : Ordinatenabweichung
Die Ableitung einer Funktion kann als Quotient zweier Differentiale aufgefasst werden.
Beispiel 13 - 14:
Gesucht ist Steigung der Sekante, also die Ordinatenänderung Δ y für eine Änderung von Δ x= 0,1 an x=1.
| Für y | = | x2 + ex−1 | in P=(1 2) |
| Für Δ x | = | 0,1 |
| Δ y | = | f(x+Δ x)−f(x) |
| | = | f(1+0,1)−f(1) | ≈ | 2,315−2≈ 0,315 |
| |
Damit ist die Steigung der Sekante im Punkt P=(1 2) ungefähr 3,15.
Steigung der Kurventangente:
Differenz der Steigungen: ms −mt ≈ 3,15 − 3 = 0,15
→ Der relative Fehler ist dann F = Steigungsdifferenz / Steigung ≈ 0,15/ 3 ≈ 5%

