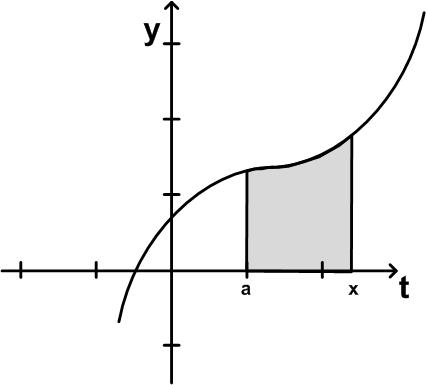
| Abbildung 75: Variation der oberen Integrationsgrenze |
Vergrößert man die obere Grenze x im Integral F(x) = ∫ax f(x)dx um Δ x, so wächst der Flächeninhalt um Δ F = F(x+ Δ x) − F(x):

Abbildung 75: Variation der oberen Integrationsgrenze
Zwischen den Flächeninhalten besteht also die Beziehung
f(x) · Δ x ≤ Δ F ≤ f(x+ Δ x ) · Δ x, und nach Division durch Δ x: .
f(x) ≤ Δ F/ Δ x ≤ f(x+ Δ x ) . .
Bildet man den Grenzübergang Δ x → 0 : .
.
limΔ x → 0 f(x) ≤ limΔ x → 0 Δ F/ Δ x ≤ limΔ x → 0 f(x + Δ x), .
.
so wird mit limΔ x → 0 Δ F/ Δ x = F′(x) .
.
und mit limΔ x → 0 f(x) = limΔ x → 0 f(x + Δ x) = f(x) : .
.
f(x) ≤ F′(x) ≤ f(x) und damit F′(x) = f(x). .
.
Dies führt zum Fundamentalsatz der Differential- und Integralrechnung:
Jedes unbestimmte Integral F(x) = ∫ax f(x)dx ist eine Stammfunktion zu f(x): .
F(x) = ∫ax f(x)dx ⇒ F′(x) = f(x) .
Beispiel 14 - 8 in9003
Gegeben sei die Funktion f(x) = e(x + 1/ x)
| f′(x) |
| ∫ | f′(x) dx |
.
.
Lösung ansehen .
.