Beispiel 16 - 33 mt9019 .
Die Matrix .
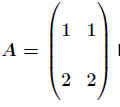 .
. .
.
Die Matrix A müßte erfüllen: A· A−1 = E
.
.
Lösung ansehen .
.
Wie bereits gezeigt, sind Matrixprodukte nicht kommutativ.
Man kann jedoch auf beiden Seiten einer Gleichung eine Multiplikation mit der gleichen Matrix durchführen (Rechts- oder Links-Multiplikation).
Hat man speziell eine Matrixgleichung mit einer einreihigen, quadratischen Matrix A
A X = E (E : Einheitsmatrix), so heißt X die zu A inverse Matrix und wird durch das Symbol A−1 dargestellt.
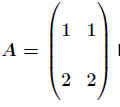 .
. .
.
Lösung ansehen .
.
Berechnung der inversen Matrix unter Verwendung von Unterdeterminanten
Für eine reguläre n-reihige (quadratische) Matrix A kann man mit Hilfe von Unterdeterminanten die Inverse A−1 wie folgt berechnen:
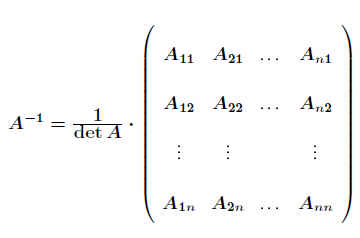 .
.
.
Man beachte die Reihenfolge der Indizes !
Aki = AikT
Aik ist das algebraische Komplement, also die mit dem Vorzeichenfaktor (−1)i+k versehene Unterdeterminante Dik :
Aik = (−1)i+k · Dik
Nachteil des Verfahrens ist der hohe Rechenaufwand bei größeren Matrizen.
Stattdessen wird eine Matrix häufig nach dem Gaußschen Algorithmus (Gauß-Jordan-Verfahren) invertiert.
Hierbei bildet man aus einer Matrix A und einer n-reihigen Einheitmatrix eine erweiterte Matrix
 .
.
.
Mit Hilfe elementarer Zeilenumformungen wird diese Matrix so umgeformt, daß auf der linken Seite die Einheitsmatrix steht. Auf der rechten Seite steht dann die Inverse:
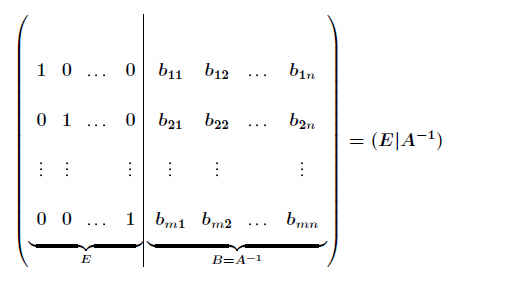 .
.
.
.
Beispiel 16 - 34 mt9028
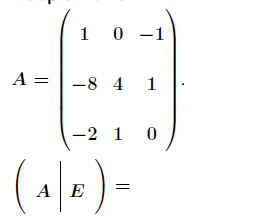 .
.
.
.
.
Lösung ansehen .
.