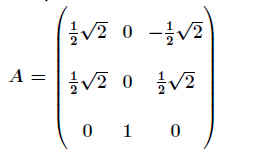16.2.8  Orthogonale Matrix

Ensteht aus dem Produkt einer n-reihigen Matrix A und ihrer Transponierten A⁻¹ eine Einheitsmatrix
A · A^T = E,
so heißt die Matrix A orthogonal.
Es gilt: .
.
.
.
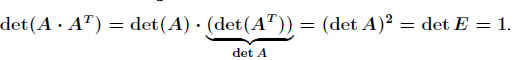Damit ist
detA = 1 oder detA = −1.
Dann gilt auch:
A · A⁻¹ = A⁻¹ · A = E .
Multipliziert man nun auf beiden Seiten von links mit der inversen Matrix A⁻¹ , so erhält man:
A⁻¹ · (A · A^T) = A⁻¹ · E und weiter
.
.
Das heißt, eine Orthogonale Matrix geht bei der Transposition in ihre inverse über. Dann gilt auch:
A · A^T = A^T · A = E.

Eigenschaften einer orthogonalen Matrix

1. Die Zeilen- bzw. Spaltenvektoren einer orthogonalen Matrix A bilden ein orthonormiertes System, stellen also zueinander orthogonale Einheitsvektoren dar (daher auch ihr Name)
2. Die Determinante einer orthogonalen Matrix A besitzt den Wert +1 oder −1:
   detA = ± 1
   Eine orthogonale Matrix ist daher stets regulär (der Umkehrschluß darf daraus nicht gezogen werden).
3. Bei einer orthogonalen Matrix A sind die Transponierte A^T und die Inverse A⁻¹ identisch: .
   A^T = A⁻¹ .
   

Beispiel für eine orthogonale Matrix: .
Beispiel 16 - 35 mt9020 .
.
.

.
.
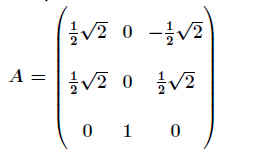Lösung ansehen .
.
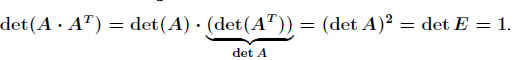