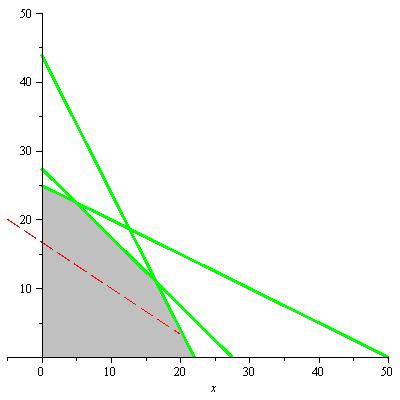
| Abbildung 89: Lösungsraum der Ungleichung |
Unter dem Begriff Lineare Optimierung (oder auch Linearer Programmierung) versteht man die Maximierung (Minimierung) einer linearen Funktion unter Nebenbedingungen in Ungleichheitsform.
Beispiel (s. Sydsaeter, Mathematik für Wirtschaftswissenschaftler) :
Ein Bäcker hat 150 kg Mehl, 22 kg Zucker und 27,5 kg Butter zur Verfügung, um zwei Arten von Kuchen zu backen. Nehmen Sie an, daß für die Produktion eines Dutzends Kuchen der Sorte A bzw. B folgende Zutaten benötigt werden: .
| Sorte | Mehl | Zucker | Butter |
| A | 3 | 1.0 | 1 |
| B | 6 | 0.5 | 1 |
.
Die Erlöse:
Ein Dutzend verkaufter Kuchen A ergibt 20 Euro , ein Dutzend verkaufter Kuchen B ergibt 30 Euro .
Wieviele Dutzend Kuchen der Sorten A (entspricht x1) und B (entspricht x2) maximieren nun den Erlös ?
Die Zielfunktion lautet:
maxz = 20 x1 + 30 x2
mit den Nebenbedingungen
| 3x1 | + | 6.0 x2 | ≤ | 150.0 |
| x1 | + | 0.5 x2 | ≤ | 22.0 |
| x1 | + | x2 | ≤ | 27.5 |
.
und den Nicht-Negativitätsbedingungen x1≥ 0 und x2 ≥ 0.
Graphisch: .

Abbildung 89: Lösungsraum der Ungleichung
.
Um die Ungleichungen besser verarbeiten zu können, werden Schlupfvariablen y1 ≥ 0, y2 ≥ 0 und y3 ≥ 0 eingeführt:
| (I1) | y1 | + | 3x1 | + | 6.0 x2 | = | 150.0 |
| (II1) | y2 | + | x1 | + | 0.5 x2 | = | 22.0 |
| (III1) | y3 | + | x1 | + | x2 | = | 27.5 |
.
Die Schlupfvariable y1 sagt z.B. aus, wieviel kg Mehl nicht verbraucht wurde.
Das Gleichungssystem hat 3 Zeilen und 5 Variablen. Entsprechend sind 2 Variablen frei wählbar.
Das Prinzip des Simplex-Verfahrens besteht darin, ausgehend von einem Eckpunkt (einer Basislösung) zu einem weiteren Eckpunkt (ebenso eine Basislösung) und damit zu immer größeren Werten von z zu gelangen, bis ein weiteres Anwachsen nicht mehr möglich ist.
Die entsprechenden Schritte in diesem Beispiel sind:
| (I2) | x2 | = | 25.0 | − | 1/2 x1 | − | 1/6 y1 |
| (II2) | y2 | = | 9.5 | − | 3/4 x1 | + | 1/12 y1 |
| (III2) | y3 | = | 2.5 | − | 1/2 x1 | − | 1/6 y1 |
| (I3) | x1 | = | 5.0 | + | 1/3 y1 | − | 2 y3 |
| (II3) | x2 | = | 22.5 | − | 1/3 y1 | + | y3 |
| (III3) | y3 | = | 5.75 | − | 1/6 y1 | + | 3/2 y3 |
| z | = | 775 | − | 10/3 y1 | − | 10 y3 |
Lösung mit Maple:
with(simplex):
cnsts := {3*x+6*y <= 150, x+0.5*y <= 22, x+y <= 27.5}:
obj := -x+y+2*z:
maximize(obj, cnsts ∪ 0 <= x, 0 <= y, 0 <= z) oder:
maximize(obj, cnsts, NONNEGATIVE)oder:
maximize(obj, cnsts)
.
Beispiel 17 - 49 lp0190
Lösen Sie mit dem Simplex-Verfahren das Optimierungsproblem:
maxz = 3x1 + 4x2
3 x1 + 2x2 ≤ 6
x1 + 4x2 ≤ 4
.
Lösung ansehen .
.