Es schließt sich die Frage an:
Ist jede lineare Gleichung lösbar?Wir schauen uns dafür beispielhaft die folgenden drei Gleichungen an:
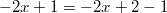
Diese lineare Gleichung ist
mehrdeutig lösbar. D. h., es gibt mehr als eine Zahl, die diese Gleichung löst. Um genau zu sein, gibt es sogar unendlich viele Lösungen. Rechnet man nämlich die Zahlen auf der rechten Seite zusammen, erhält man
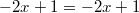
. Hier sieht man deutlich: Egal, welche Zahl man für

einsetzt, man erhält immer auf beiden Seiten das gleiche Ergebnis. Was sollte auch sonst passieren, wenn die beiden Seiten der Gleichung identisch sind?
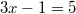
Diese lineare Gleichung ist
eindeutig lösbar. D. h., es gibt genau eine Zahl, die diese Gleichung löst. Formt man sie um, indem man erst
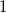 addiert
addiert und anschließend durch
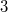 teilt
teilt, erhält man nämlich
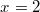
. Dies ist die einzige Lösung, denn keine andere Zahl ergibt
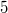
, wenn man sie mit
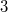 multipliziert
multipliziert und anschließend
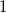 subtrahiert
subtrahiert.
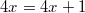
Die lineare Gleichung ist
nicht lösbar. D. h., es gibt keine Zahl, die diese Gleichung löst. Zieht man auf beiden Seiten
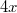
ab, was laut der Liste der Äquivalenzumformungen oben erlaubt ist, erhält man
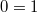
. Das ist ein Widerspruch.
Zusammenfassung: Lineare Gleichungen können nicht lösbar, eindeutig lösbar oder mehrdeutig lösbar mit unendlich vielen Lösungen sein. Andere Möglichkeiten gibt es nicht.
 Brückenkurs
Brückenkurs