Brotkrumen-Navigation

Brückenkurs » 3 Bruchrechnung

  Brückenkurs

zurückErklärungen 
  Aufgabenweiter

Lösungen

1. Aufgabe

1) \frac{4}{5}=\frac{4 \cdot 3}{5 \cdot 3}=\frac{12}{15}

2) \frac{1}{10}=\frac{1 \cdot 12}{10 \cdot 12}=\frac{12}{120}

3) \frac{7}{12}=\frac{7 \cdot 5}{12 \cdot 5}=\frac{35}{60}

4) \frac{583}{15}=\frac{583 \cdot 10}{15 \cdot 10}=\frac{5.830}{150}

5) \frac{2}{3}=\frac{2 \cdot 21}{3 \cdot 21}=\frac{42}{63}

6) \frac{123}{456}=\frac{123 \cdot 100}{456 \cdot 100}=\frac{12.300}{45.600}

2. Aufgabe

1) \frac{10}{13}=\frac{10 \cdot 3}{13 \cdot 3}=\frac{30}{39} \mbox{ } und \frac{2}{3}=\frac{2 \cdot 13}{3 \cdot 13}=\frac{26}{39}


2) \frac{8}{9}=\frac{8 \cdot 5}{9 \cdot 5}=\frac{40}{45} und \frac{4}{15}=\frac{4 \cdot 3}{15 \cdot 3}=\frac{12}{45}


3) \frac{1}{8}=\frac{1 \cdot 3}{8 \cdot 3}=\frac{3}{24} und \frac{5}{6}=\frac{5 \cdot 4}{6 \cdot 4}=\frac{20}{24}


4) \frac{99}{12}=\frac{99 \cdot 3}{12 \cdot 3}=\frac{297}{36} und \frac{5}{18}=\frac{5 \cdot 2}{18 \cdot 2}=\frac{10}{36}


5) \frac{11}{20}=\frac{11 \cdot 19}{20 \cdot 19}=\frac{209}{380} und \frac{2}{19}=\frac{2 \cdot 20}{19 \cdot 20}=\frac{40}{380}


6) \frac{1}{2}=\frac{1 \cdot 10}{2 \cdot 10}=\frac{10}{20} und \frac{1}{20} und \frac{3}{10}=\frac{3 \cdot 2}{10 \cdot 2}=\frac{6}{20}


7) \frac {1}{3}=\frac{1 \cdot 220}{3 \cdot 220}=\frac{220}{660} und \frac{7}{20}=\frac{7 \cdot 33}{20 \cdot 33}=\frac{231}{660} und \frac{2}{11}=\frac{2 \cdot 60}{11 \cdot 60}=\frac{120}{660}


8) \frac {1}{2}=\frac{1 \cdot 90}{2 \cdot 90}=\frac{90}{180} und \frac{1} {3}=\frac{1 \cdot 60}{3 \cdot 60}=\frac{60}{180} und \frac{1} {4}=\frac{1 \cdot 45}{4 \cdot 45}=\frac{45}{180} und \frac{1} {5}=\frac{1 \cdot 36}{5 \cdot 36}=\frac{36}{180} und \frac{1} {6}=\frac{1 \cdot 30}{6 \cdot 30}=\frac{30}{180} und \frac{1} {15}=\frac{1 \cdot 12}{15 \cdot 12}=\frac{12}{180} und \frac{1} {36}=\frac{1 \cdot 5}{36 \cdot 5}=\frac{5}{180}

3. Aufgabe

1) \frac{10}{18}=\frac{10 : 2}{18 : 2}=\frac{5}{9}

2) \frac{51}{17}=\frac{51 : 17}{17 : 17}=3

3) \frac{38}{171}=\frac{38 : 19}{171 : 19}=\frac{2}{9}

4) \frac{30}{205}=\frac{30 : 5}{205 : 5}=\frac{6}{41}

5) \frac{23}{30}

Bemerkung: 23 und 30 enthalten keine gemeinsamen Teiler. Also kann man diesen Bruch nicht kürzen.


6) \frac{124.000}{987.000}=\frac{124.000 : 1.000}{987.000 : 1.000}=\frac{124}{987}

4. Aufgabe

1) \frac{67}{6}=\frac{66}{6}+\frac{1}{6}=11\frac{1}{6}

2) \frac{25}{23}=\frac{23}{23}+\frac{2}{23}=1\frac{2}{23}

3) \frac{94}{24}=\frac{72}{24}+\frac{22}{24}=3\frac{22}{24}=3\frac{11}{12}

4) \frac{119}{17}=7

5) \frac{235}{50}=\frac{200}{50}+\frac{35}{50}=4\frac{35}{50}=4\frac{7}{10}

6) 2\frac{1}{9}=\frac{18}{9}+\frac{1}{9}=\frac{19}{9}

7) 1\frac{13}{14}=\frac{14}{14}+\frac{13}{14}=\frac{27}{14}

8) 8\frac{4}{7}=\frac{56}{7}+\frac{4}{7}=\frac{60}{7}

9) 10\frac{10}{15}=\frac{150}{15}+\frac{10}{15}=\frac{160}{15}=\frac{32}{3}

10) 5\frac{20}{33}=\frac{165}{33}+\frac{20}{33}=\frac{185}{33}

5. Aufgabe

Wichtig: Bei allen Multiplikations- und Divisionsaufgaben, in denen gemischte Zahlen enthalten sind, muss die gemischte Zahl vor dem Multiplizieren bzw. Dividieren in einen unechten Bruch umgewandelt werden, sonst kommen anschließend Punkt- und Strichrechnung durcheinander...
Zur Wiederholung: Dies ist die einzige Stelle in der Mathematik, bei der nicht ein Malzeichen, sondern ein Pluszeichen weggelassen wird. Steht in einer Aufgabe z. B. die gemischte Zahl 1\frac{1}{2}, ist damit die Summe 1+\frac{1}{2} gemeint. Diese Schreibweise verkompliziert Rechnungen also eher bzw. macht sie fehleranfälliger. Sie wird in diesem Lernmodul auch nur eingeführt, weil z. B. einige Taschenrechner sie verwenden und es deswegen nötig ist, zu verstehen, wie sie gelesen werden muss.


1) \frac{3}{4} \, + \, \frac{3}{2} \, = \, \frac{3}{4} \, + \, \frac{3 \cdot 2}{2 \cdot 2} \, = \, \frac{3}{4} \, + \, \frac{6}{4} \, = \, \frac{9}{4} \, = \, 2\frac{1}{4}


2) 1 \frac{5}{6} \, + \, 2 \frac{7}{8} \, = \, \frac{6}{6} \, + \, \frac{5}{6} \, + \, \frac{16}{8} \, + \, \frac{7}{8} \, = \, \frac{11}{6} \, + \, \frac{23}{8} \, = \, \frac{11 \cdot 4}{6 \cdot 4} \, + \, \frac{23 \cdot 3}{8 \cdot 3} \, = \, \frac{44}{24} \, + \, \frac{69}{24} \, = \, \frac{113}{24} \, = \, 4 \frac{17}{24}


3) \frac{3}{2} \, + \, 12 \, = \, \frac{3}{2} \, + \, \frac{24}{2} \, = \, \frac{27}{2}\, = \, 13 \frac{1} {2}


4) \frac{1}{7} \, - \, \frac{3}{5} \, = \, \frac{1 \cdot 5}{7 \cdot 5} \, - \, \frac{3 \cdot 7}{5 \cdot 7} \, = \, \frac{5}{35} \, - \, \frac{21}{35} \, = \, - \frac{16}{35}


5) 4 \frac{2}{9} \, - \, 1 \frac{1}{3} \, = \, \frac{36}{9} \, + \, \frac{2}{9} \, - \, \left( \frac{3}{3} \, + \, \frac{1}{3} \right) \, = \, \frac{38}{9} \, - \, \frac{4}{3} \, = \, \frac{38}{9} \, - \, \frac{4 \cdot 3}{3 \cdot 3} \, = \, \frac{38}{9} \, - \, \frac{12}{9} \, = \, \frac{26}{9} \, = \, 2 \frac{8}{9}


6) 4 \, \cdot \, \frac{2}{3} \, \cdot \frac{5}{8} \, = \, \frac{5}{3} \, = \, 1\frac{2}{3}

Bemerkung: Vor dem Multiplizieren wurden hier die 4 und die 2 (Zähler vom zweiten Bruch) mit der 8 (Nenner vom dritten Bruch) gekürzt.


7) 2\frac{1}{4} \, \cdot \, \frac{2}{7} \, = \, \frac{9}{4} \, \cdot \, \frac{2}{7} \, = \, \frac{9}{2} \, \cdot \, \frac{1}{7} \, = \, \frac{9}{14}

Bemerkung: Vor dem Multiplizieren wurden hier die 4 (Nenner vom ersten Bruch) mit der 2 (Zähler vom zweiten Bruch) durch 2 gekürzt.


8) \frac{7}{9} \cdot 6 = \frac{7}{9} \cdot \frac{6}{1} = \frac{7}{3} \cdot \frac{2}{1} = \frac{14}{3} = 4 \frac{2}{3}

Bemerkung: Vor dem Multiplizieren wurden hier die 9 (Nenner vom ersten Bruch) mit der 6 (Zähler vom zweiten Bruch) durch 3 gekürzt.


9) \frac{3}{8} \, : \, \frac{5}{4} \, = \, \frac{3}{8} \, \cdot \, \frac{4}{5} = \frac{3}{2} \, \cdot \, \frac{1}{5} = \frac{3}{10}

Bemerkung: Vor dem Multiplizieren wurden hier die 8 (Nenner vom ersten Bruch) mit der 4 (Zähler vom zweiten Bruch) durch 4 gekürzt.


10) \frac{5}{6} \, : \, \frac{25}{12} \, = \, \frac{5}{6} \, \cdot \, \frac{12}{25} \, = \frac{1}{1} \, \cdot \frac{2}{5} \, = \, \frac {2}{5}

Bemerkung: Vor dem Multiplizieren wurden hier die 5 (Zähler vom ersten Bruch) mit der 25 (Nenner vom zweiten Bruch) durch 5 sowie die 6 (Nenner vom ersten Bruch) mit der 12 (Zähler vom zweiten Bruch) durch 6 gekürzt.


11) 4\frac{2}{5} \, : \, 3\frac{1}{10} \, = \, \frac{22}{5} \, : \, \frac{31}{10} \, = \, \frac{22}{5} \, \cdot \, \frac{10}{31} \, = \, \frac{44}{31}

Bemerkung 1: Vor dem Multiplizieren wurden hier die 5 (Nenner vom ersten Bruch) mit der 10 (Zähler vom zweiten Bruch) durch 5 gekürzt.


12) 5 : \frac{10}{13} = \frac{5}{1} \cdot \frac{13}{10} = 1 \cdot \frac{13}{2} = 6 \frac{1}{2}

Bemerkung: Vor dem Multiplizieren wurden hier die 5 (Zähler vom ersten Bruch) mit der 10 (Nenner vom zweiten Bruch) durch 5 gekürzt.

6. Aufgabe

Bemerkung 1: Grundsätzlich sind diese Aufgaben nicht eindeutig zu lösen. Neben der Anforderung, dass die Rechnungen stimmen sollen, ist daher die Vorgabe, dass möglichst kleine Ziffern gefunden werden sollen, entscheidend. Ein bisschen "Rumprobieren" wird aber auch so nötig sein.
Bemerkung 2: Auch wenn z. B. im Zähler "nur" ein Sternchen steht, muss dieses beim Erweitern mit der entsprechenden Zahl multipliziert werden, weil erweitern nun mal heißt "Zähler und Nenner mit der gleichen Zahl multiplizieren". Das gilt auch für Sternchen...

1)
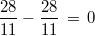1. Überlegung: Damit eine Differenz 0 ergibt, müssen Minuend und Subtrahend gleich sein. Die naheliegendste Lösung ist also \frac{28}{11}-\frac{28}{11} \, = \, 0

Bemerkung: Dies ist aber nicht die einzige Lösung, z. B. stimmt auch \frac{14}{11}-\frac{28}{22} \, = \, 0 . Und es kann nochmal nicht mal entschieden werden, welche Zahlenkombination die kleinere ist...


2)
1. Überlegung: Da beim Multiplizieren von Brüchen jeweils die Zähler und die Nenner multipliziert werden, können sie separat betrachtet werden.

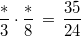2. Überlegung: Im Nenner muss einfach nur multipliziert werden: 3 \cdot 8=24 , also ist \frac{*}{3}\cdot \frac{*}{8} \, = \, \frac{35}{24}

3. Überlegung: Die 35 im Zähler des Bruches auf der rechten Seite kann im Bereich der natürlichen Zahlen nur auf genau eine Weise in Faktoren zerlegt werden, nämlich 35=5 \cdot 7 . Es kann allerdings nicht entschieden werden, welcher Faktor an erster und welcher Faktor an zweiter Stelle in der ursprünglichen Rechnung steht. Es gibt daher zwei Lösungen.

Lösung: \frac{5}{3}\cdot \frac{7}{8} \, = \, \frac{35}{24} oder \frac{7}{3}\cdot \frac{5}{8} \, = \, \frac{35}{24}


3)
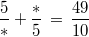1. Überlegung: Einfacher wird die Rechnung, wenn die gemischte Zahl auf der rechten Seite in einen unechten Bruch umgewandelt wird. Es ergibt sich: \frac{5}{*}+\frac{*}{5} \, = \, \frac{49}{10}

2. Überlegung: Die kleinste Ziffer, die für den Nenner des ersten Bruches infrage kommt, ist 1 . 0 scheidet ja als Kandidat für einen Nenner aus. Er ergibt sich: \frac{5}{1}+\frac{*}{5} \, = \, \frac{49}{10}

3. Überlegung: Das lässt sich umformen zu \frac{*}{5} \, = \, \frac{49}{10}-5 oder \frac{*}{5} \, = \, -\frac{1}{10} . Dies ist (mathematisch gesprochen) die Frage, welche Zahl ergibt -\frac{1}{10} , wenn man sie durch 5 teilt. Eigentlich muss man an dieser Stelle gar nicht weiterrechnen, weil nur eine negative Zahl hier für ein richtiges Ergebnis sorgen kann: Eine positive Zahl geteilt durch eine andere positive Zahl (und die 5 ist ja hier als positive Zahl schon vorgegeben) wäre ja wieder positiv und nicht -\frac{1}{10} . Damit kann man die Vorgabe, dass für die Sternchen Ziffern eingesetzt werden sollen, nie erfüllen. Für diejenigen, die das genaue Ergebnis in diesem Fall wissen möchten: Für das Sternchen müsste -\frac{1}{2} eingesetzt werden, damit die Rechnung stimmt, was auch deswegen nicht funktioniert, weil es nicht ganzzahlig ist.

4. Überlegung: Probieren wir es also mit der nächstgrößeren Ziffer 2 . Wir bekommen: \frac{5}{2}+\frac{*}{5} \, = \, \frac{49}{10} oder (wenn wir alles auf den Hauptnenner bringen) \frac{25}{10}+\frac{2\cdot *}{10} \, = \, \frac{49}{10}

5. Überlegung: Da die Nenner nun gleich sind, können wir sie für den folgenden Schritt ignorieren. Es ergibt sich: 25+2\cdot *=49 . Daraus folgt: 2 \cdot *=24 und damit *=12

Lösung: \frac{5}{2}+\frac{12}{5} \, = \, 4\frac{9}{10}


4)
1. Überlegung: Die beiden Sternchen auf der rechten Seite müssen für 45 stehen, da dies der Hauptnenner von 5 und 9 ist. Es ergibt sich: \frac{1}{5}-\frac{*}{9} \, = \, -\frac{1}{45} oder, wenn man gleich alles auf den Hauptnenner bringt, \frac{9}{45}-\frac{5\cdot *}{45} \, = \, -\frac{1}{45}

2. Überlegung: Da die Nenner nun gleich sind, können wir sie wieder ignorieren. Bleibt die Frage: 9-5\cdot *=-1 , die uns zu der Erkenntnis führt, dass 5\cdot * offensichtlich gleich 10 sein muss. Wenn 5 \cdot *=10 ist, ist *=2

Lösung: \frac{9}{45}-\frac{10}{45} \, = \, -\frac{1}{45} oder \frac{1}{5}-\frac{2}{9} \, = \, -\frac{1}{45}


5)
1. Überlegung: Auf der rechten Seite hat das Sternchen im Nenner keine Auswirkungen auf die Rechnung, egal durch welche Zahl die 0 im Zähler geteilt wird, das Ergebnis ist immer 0 . Da eine möglichst kleine Ziffer gefordert war, können wir die 1 für dieses Sternchen nehmen - oder es einfach weglassen.

2. Überlegung: Damit das Ergebnis insgesamt 0 ist, müsste auf der linken Seite eine der Zahlen negativ sein, denn die Summe von zwei positiven Zahlen ist wieder positiv. Negative Zahlen haben wir aber wegen der Einschränkung, dass Ziffern gesucht sind, nicht zur Verfügung. Insofern lassen sich hier keine passenden Zahlen finden.


6)
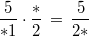1. Überlegung: Man teilt durch einen Bruch, indem man mit dem Kehrwert multipliziert. Das bedeutet hier: \frac{5}{*1} \cdot \frac{*}{2} \, = \, \frac{5}{2*}

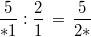2. Überlegung: Schauen wir uns die Rechnung im Zähler an: 5\cdot *=5 . Also muss dieses Sternchen gleich 1 sein. Es ergibt sich: \frac{5}{*1} \cdot \frac{1}{2} \, = \, \frac{5}{2*} bzw. in der Originalrechnung: \frac{5}{*1} : \frac{2}{1} \, = \, \frac{5}{2*}

3. Überlegung: Für den Nenner folgt daraus: *1\cdot 2=2* . Für das rechte Sternchen berechnet man 1 \cdot 2 = 2; für das linke umgekehrt. Das Ergebnis ist also 11\cdot 2=22

Lösung: \frac{5}{11} : \frac{2}{1} \, = \, \frac{5}{22} . Dafür kann man natürlich auch \frac{5}{11} : 2 \, = \, \frac{5}{22} schreiben.
zurückErklärungen 
  Aufgabenweiter