8.2.1 Umkehrbarkeit
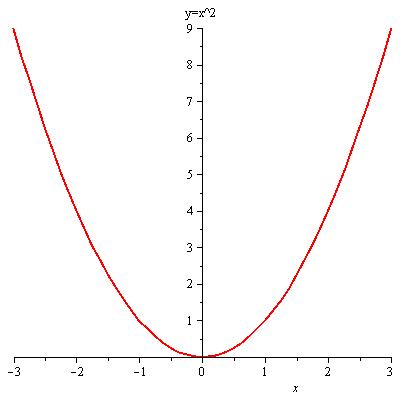
Quadtratische Funktionen sind nicht umkehrbar, solange ⅅ=(−∞<x<∞)
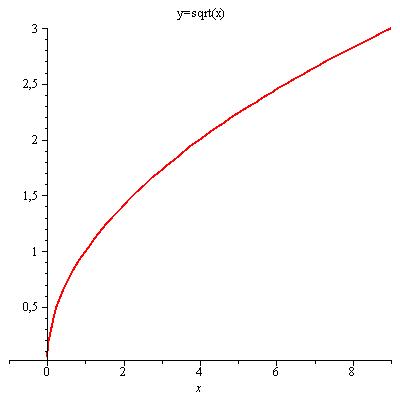
| Abbildung 17: Umkehrbarkeit für x≥ 0 → y=√x |
⇒ Jede Potenzfunktion mit geradem Exponent ist im Intervall x≥ 0 umkehrbar.
Die Umkehrfunktionen der auf das Intervall x≥ 0 beschränkten Funktionen heißen Wurzelfunktionen :
Beispiel 8 - 28: Maple-Befehl sqrt()
liefert den Wert der Quadratwurzel. ’sqrt(4)’; ergibt 2.
Beispiel 8 - 29: n-te Wurzel
Gesucht ist die n-te Wurzel einer reellen Zahl: (x)1/n.
Umgesetzt in den Maple-Befehl ’surd(x,n)’ erhält man das Ergebnis.
Zahlenwerte:
∛27 . ’surd(27,3)’ liefert: 3
Beispiel 8 - 30: Maple-Befehl isolate
unterstützt bei der Bildung von Umkehrfunktionen:
isolate(y=sqrt(x),x)
isolate(y=x−1/2,x)
(vgl. auch solve)