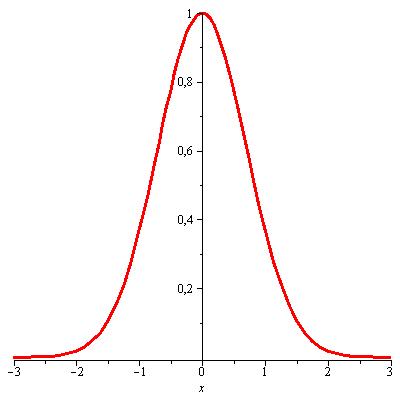
| Abbildung 22: Gauß-Funktion |
Die Gauß-Funktion ist von der Form y=e−x2, .
allgemein: y=a· e−b(x−x0)2. .

Abbildung 22: Gauß-Funktion
.
Häufig wird die Gauß-Funktion bei statistischen Betrachtungen eingesetzt. Die Verteilungsdichte wird beschrieben als: .
f(x) = 1/ σ √ 2 π· e−(1/2( x−µ/σ)2. .
Bei dieser Schreibweise lassen sich einige Kenngrößen gut angeben: .
Die Standardabweichung σ beschreibt die Breite der Normalverteilung und hängt mit der Halbwertsbreite zusammen. Berücksichtigt man die tabellierten Werte der Verteilungsfunktion, gilt näherungsweise folgende Aussage: .