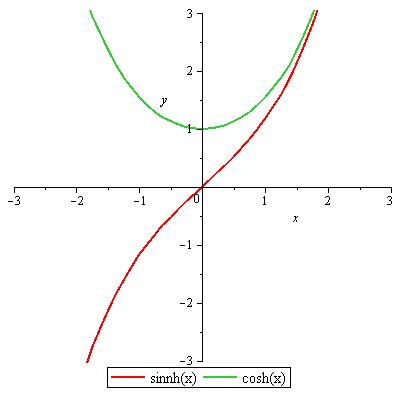
| Abbildung 40: sinh und cosh |
Die Begriffe Hyperbelfunktion , Hyperbelsinus sowie Hyperbelcosinus leiten sich aus der Beziehung
cosh2(x) − sinh2(x) = 1 ab, die ähnlich zu
sin2(x) + cos2(x) = 1 ist.
Beispiel 12 - 23 tf9014
cosh2 λ − sinh2 λ = .
.
.
Lösung ansehen .
.
sinhx = (ex−e−x)/ 2
coshx = (ex+e−x)/ 2

Abbildung 40: sinh und cosh
.
tanhx= sinhx/ coshx
cothx= coshx/ sinhx
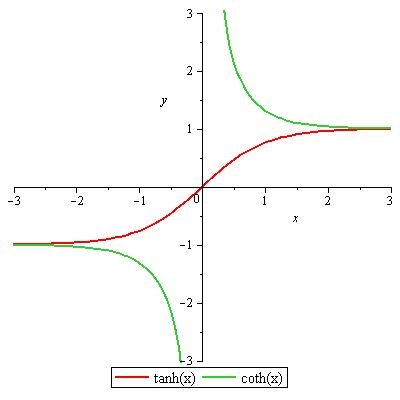
Abbildung 41: tanh und coth
Additionstheoreme :
| sinh(x1 ± x2) | = | sinhx1· coshx2± coshx1·sinhx2 |
| cosh(x1 ± x2) | = | coshx1· coshx2± sinhx1·sinhx2 |
| tanh(x1 ± x2) | = | (tanhx1 ± tanhx2)/ (1±tanhx1tanhx2) |
⇒
| cosh2x − sinh2x | = | 1 |
| sinh2x | = | 2sinhx coshx |
| cosh2x | = | sinh2x + cosh2x |
| coshx + sinhx | = | ex |
| coshx − sinhx | = | e−x |
Technische Anwendung: Die Kettenlinie .
Beispiel 12 - 24 tf9015
Kettenlinien werden durch eine Funktion
y= a cosh( x/ a) beschrieben. .
Zwei Masten sind 40 m voneinander entfernt. Eine Leitung (=’Kette’) zwischen diesen zwei Befestigungen hat in der Mitte einen Abstand von 10 m zum Erdboden. Wie hoch sind die Masten ?. .
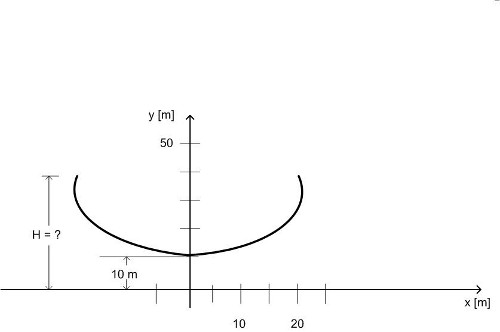
Abbildung 42: Kettenlinie
.
.
.
Lösung ansehen .
.
.
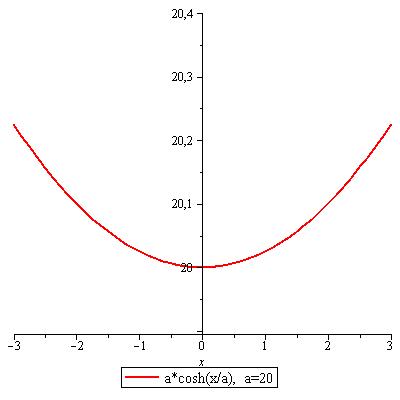
Abbildung 43: Kettenlinie
Beispiel 12 - 25: ″ Freier ″ Fall mit Luftwiderstand
| R | = | k· v2 | Reibungskraft, mit k ≈ const. | |
| G | = | m· g | ||
| VE | = | √mg/k | ||
| v(t) | = | ve·tanh( mg/ (ve· t) | ||
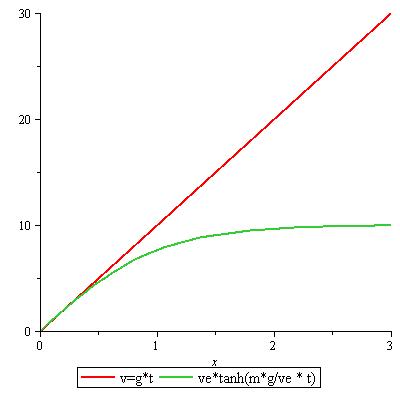
Abbildung 44: Fall mit Luftwiderstand