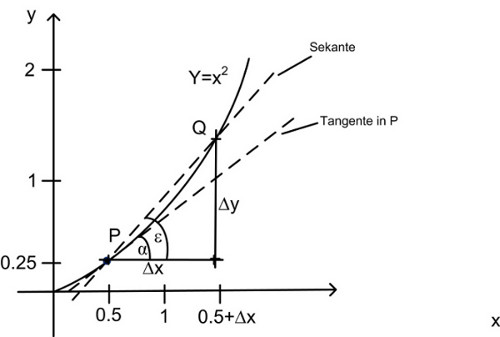
| Abbildung 46: Tangentenproblem |
Beispiel:
| y | = | f(x) | = | x2 | x | = | 0,5 | : | Steigung | |

Abbildung 46: Tangentenproblem
.
Gesucht ist zunächst die Steigung der Sekante ms:
| ms | = | tanε | = | Δ y/ Δ x | |
| = | ((0,5+Δ x)2−0,25)/ Δ x | = | (0,25+Δ x + Δ x2 −0,25)/ Δ x | ||
| = | (Δ x · (1 + Δ x))/ Δ x | = | 1 + Δ x | ||
Für die Tangentensteigung gilt:
| Δ x → 0 | mt | = | tanα | = | limΔ x → 0 Δ y/ Δ x |
| = | limΔ x → 0(1+Δ x) | = | 1 | ||
.
Der Grenzwert existiert und ist links und rechts gleich.
⇒ Funktion ist an der Stelle x=0,5 differenzierbar.
Den angegebenen Grenzwert bezeichnet man als Ableitung :
| mt | = | tanα | = | limΔ x → 0 (f(x0+Δ x) − f(x))/ Δ x |
.
Sie wird häufig wie folgt symbolisiert: .
| y′(x0), | f′(x0), | dy/dx|x=x0Differentialquotient | ||
Differenzierbarkeit -auch innerhalb des Definitionsbereichs- ist nicht von vornherein gegeben; Beispielsweise ist die Funktion
| y=|x|= | ⎧ ⎨ ⎩ |
|
.
nicht überall ableitbar: An der Stelle x = 0 besitzt sie keine eindeutig bestimmte Tangente:
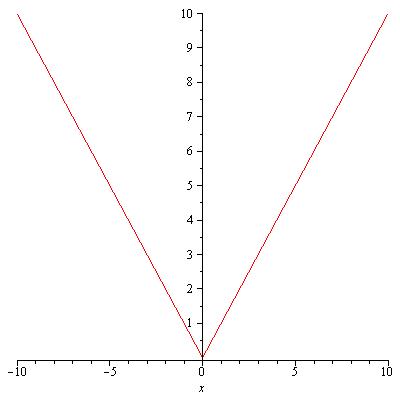
Abbildung 47: Differenzierbarkeit von y=|x|
.. .
Die Funktion y=|x| ist an der Stelle x=0 nicht differenzierbar