13.3.1  Tangente und Normale

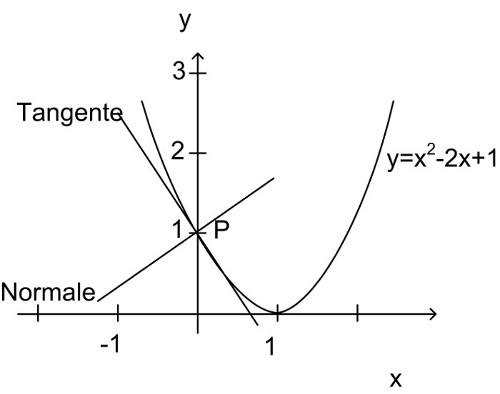
Abbildung 50: Tangente und Normale

Tangentengleichung:

y−y0
x−x0
=f′(x0)=mt


Steigung der Normalen:

mn=−
 1
 mt

Normalengleichung:

y−y0
x−x0
=
−1
f′(x0)

Beispiel 13 - 17:
y=x2−2x+1
gesucht: Gleichung der Tangente und Normale n am Schnittpunkt mit der y-Achse.
Schnittpunkt mit der y-Achse: .

P=⎛
⎝		0 1⎞
⎠


Tangentensteigung:

y′=2x−2

.

mt= y′(0)= −2

.
Tangente:

y−1
x−0
=−2

.

y=−2x+1

.
Normale: .

  y−1
  x−0
=
  1
  2

.

y=
  1
  2
x+1

.

.
Beispiel 13 - 18 df9011 .
Zu ermitteln ist die Gleichung der Tangente, die vom Punkt A=(0; −1) aus an den Funktionsgraphen y = lnx gelegt wird.

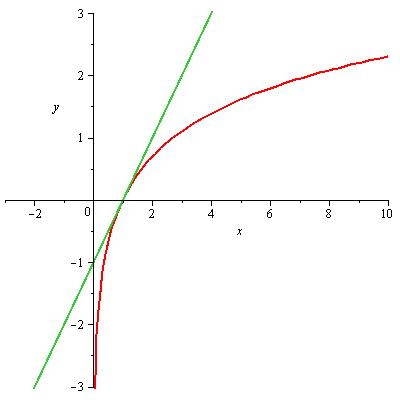
Abbildung 51: Tangenten an Funktionen

.
.
Lösung ansehen .
.