13.3.2  Charakteristische Kurvenpunkte, Monotonie

1. Monotonie

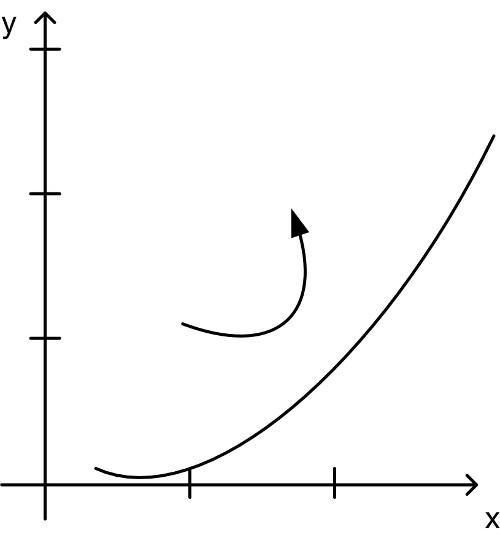
   f′(x0) > 0	Funktionskurve steigt streng monoton beim Durchgang durch x0
   f′(x0) ≥ 0	Funktionskurve steigt monoton beim Durchgang durch x0
   f′(x0) < 0	Funktionskurve fällt streng monoton beim Durchgang durch x0
   f′(x0) ≤ 0	Funktionskurve fällt monoton beim Durchgang durch x0

   
   Beispiel 13 - 19:
   

   ---

   

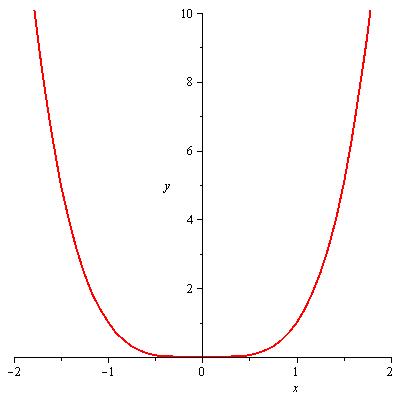
   Abbildung 52: Monotonie

   ---

   y	=	x4
   y′	=	4x3	{<0 für x <0 >0 für x >0

   
   .
   Beispiel 13 - 20 df9012 .
   

   y	=	x3+2x

   
   

   .
   .
   Lösung ansehen .
   .
   

   .
   .
   Beispiel 13 - 21 df9013 .
   

   y	=	|x2−2x+1|	(x≥ 1)

   
   

   .
   .
   Lösung ansehen .
   .
   

2. 2. Ableitung, Krümmung

   ---

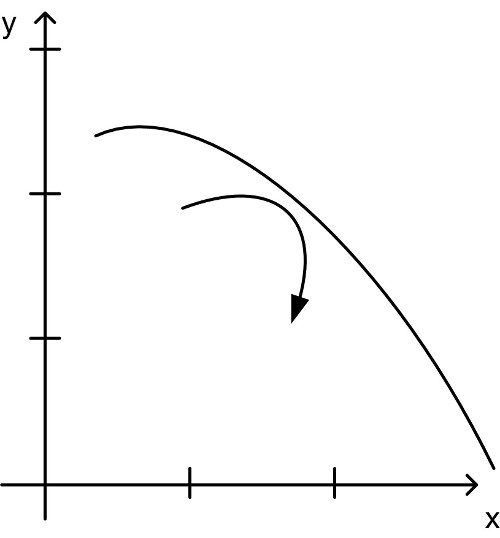
   f″(x) > 0	f″(x) < 0
   Linkskrümmung	Rechtskrümmung
   konvex	konkav

   
   

   Abbildung 53: Krümmung

   ---

   Krümmung

   k=	f″(x)    ⎛ ⎝ 1+f′(x)2 ⎞ ⎠ 3 2

   
   Beispiel 13 - 22 df9014
   Kreisgleichung, obere Hälfte
   

   y	=	√r2−x2	=	(r2−x2)1/2

   
   .
   .
   Lösung ansehen .
   .
   

   Krümmung

   k=−

   1   r

   (Kehrwert des Radius)
   
   Allgemein gilt: Krümmungsradius

   ρ =

   1 |k|