15.1.2 Einige Beispiele zum Einstieg
Beispiel 15 - 1:
In der Klasse 7c sind 31 Schüler. Die Zahl der Mädchen ist um 3 kleiner als die Zahl der Jungen. Wie viele Jungen und Mädchen sind in der Klasse ?
| M: Mädchen | | J: Jungen |
| M+J | = | 31 |
| M+3 | = | J |
Beispiel 15 - 2:
Drei Zahnräder eines Getriebes haben zusammen 80 Zähne. Bei 10 Umdrehungen des ersten Rades drehen sich das zweite 18 und das dritte 45 mal. Wie viel Zähne hat jedes Rad ?
| A+B+C | = | 80 |
| A/ 18 | = | B/ 10 |
| A/ 45 | = | C/ 10 |
Beispiel 15 - 3: Balken in einem Lager
Ein Balken (Länge k) wird in einem festen Lager links eingespannt und rechts von einem Seil in einem Winkel von 45 1exo gehalten. Eine Kraft F wirkt unter dem Winkel α auf die Mitte des Balkens.
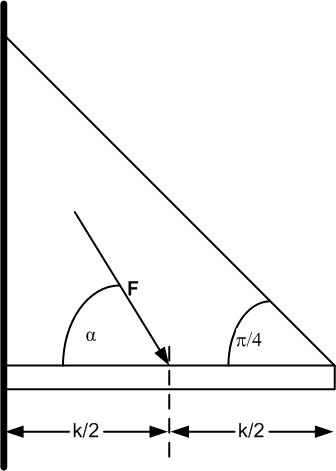
| Abbildung 84: Eingespannter Balken |
Fragestellung der Technischen Mechanik ist bei diesem Beispiel die Bestimmung der Kräfte FA, FB und des Moments MA in Abhängigkeit vom Winkel α der angreifenden Kraft F (’Drehachse’ links): .
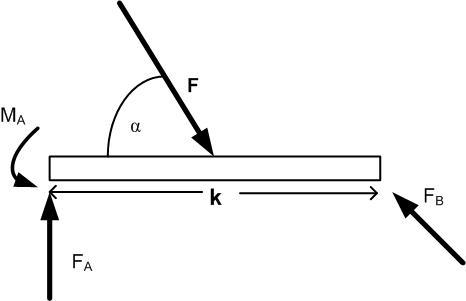
| Abbildung 85: Kräfte an einem Balken |
.
| x−Richtung : | 0· FA | + | | + | 0· MA | = | F · cosα |
| y−Richtung : | FA | + | | + | 0· MA | = | F · sinα |
| Drehmoment M : | 0· FA | + | | + | MA | = | |
.
.
⇒ 3 Gleichungen, 3 Unbekannte .
Beispiel 15 - 4: Verschnittkreuz
Gegeben sind die zwei (zu bestimmenden) Mengen x1 und x2 eines Weins mit dem Säuregehalt G1=3,8 g/l und G2=9 g/l, die zusammengemischt werden sollen zu einer (evtl. unbekannten) Gesamtmenge M und einem Gesamtsäuregehalt G= 6 g/l.
Die Gleichungen dieses Systems lauten dann:
| x1 | + | x2 | = | M |
| G1 · x1 | + | G2 · x2 | = | G · M |
Nun multipliziert man die erste Gleichung mit G2:
| G2 · x1 | + | G2 · x2 | = | G2 · M |
| G1 · x1 | + | G2 · x2 | = | G · M |
Subtraktion der zweiten von der ersten Zeile ergibt:.
| (G2−G1) · x1 | + | | = | (G2 − G) · M |
und damit
oder x1 ∝ G2 − G
Die gleichen Schritte werden nach der Multiplikation der ersten Gleichung mit G1 analog durchgeführt:
| G1 · x1 | + | G1 · x2 | = | G1 · M |
| G1 · x1 | + | G2 · x2 | = | G · M |
Subtraktion der zweiten von der ersten Zeile ergibt:.
| | + | (G2−G1) · x2 | = | (G − G1) · M |
und damit x2 = (G − G1) · M/G2−G1
oder x2 ∝ G − G1.
Kennt man die gesuchte Gesamtmenge nicht, kann man für das Verhältnis von x1 zu x2 angeben:
| = | | = | | (9.0 − 6.0)g/l |
|
| (6.0−3.8) g/l |
| = | | ≈ 1.36 |
.
Zum besseren Behalten dieser Gleichungen werden die Werte in einem (Verschnitt-)Kreuz aufgetragen:
| G1 | | x1 ∝(G2−G) |
| | G | |
| G2 | | x2 ∝(G−G1) |
.
.
Mit Zahlen: .
.
.
.
Hat man nun eine vorgegebene Menge x1=630 l, so kann man die Menge des Weins x2 einfach bestimmen zu:
und
.
Lösung des Beispiels mit Maple:
restart;
eq1 := x1+x2 = M;
eq2 := 3.8*x1+9*x2 = 6.0*M;
solve({eq1, eq2}, {x1, x2,M}) ergibt:
x1 + x2 = M
3.8 x1 + 9 x2 = 6.0 M
{M = 2.363636364*x2, x1 = 1.363636364*x2, x2 = x2}.
Also: x2 ist frei wählbar, daraus ergibt sich x1 und daraus wiederum die Gesamtmenge.
Beispiel 15 - 5 mt9001
Gegeben sind die drei (zu bestimmenden) Mengen x1, x2 und x3 eines Weins mit dem Alkoholgehalt A1=8 Vol %, A2=12 Vol % und A3=15 Vol % , die zusammengemischt werden sollen zu einer (evtl. unbekannten) Gesamtmenge M und einem Gesamt-Alkoholgehalt A= 12 Vol %.
(1.267 l Alkohol entspricht 1 kg; auf der linken und rechten Seite steht aber der gleiche Faktor.)
Gleichzeitig haben die Weine Säuregehalte von S1=3 g/l, S2=9 g/l und S3=5 g/l,die zusammengemischt den Ziel-Gesamtsäuregehalt G= 6 g/l haben sollen.
.
.
Lösung ansehen .
.
Beispiel 15 - 6 mt9002
Gegeben sind die drei (zu bestimmenden) Mengen x1, x2 und x3 eines Weins mit dem Alkoholgehalt A1=8 Vol %, A2=12 Vol % und A3=13,5 Vol % , die zusammengemischt werden sollen zu einer (evtl. unbekannten) Gesamtmenge M und einem Gesamt-Alkoholgehalt A= 12 Vol %.
(1.267 l Alkohol entspricht 1 kg; auf der linken und rechten Seite steht aber der gleiche Faktor.)
Gleichzeitig haben die Weine Säuregehalte von S1=3,8 g/l, S2=9 g/l und S3=7 g/l,die zusammengemischt den Ziel-Gesamtsäuregehalt G= 6 g/l haben sollen.
.
.
Lösung ansehen .
.
Die Systematik von linearen Gleichungssytemen kann diese Ergebnisse erklären.


