15.4.1  Darstellung in Matrixform

.
.


.
Das lineare Gleichungssystem kann geschrieben werden als A · x→ = c→ .
nz Koeffizienten: aik
Absolutglieder (Konstanten): ci

A · x→ = c→ ⇒

a11· x1+ a12· x2+ a13· x3+ ⋯ + a1n· xn=c1
a21· x1+ a22· x2+ a23· x3+ ⋯ + a2n· xn=c2
a31· x1+ a32· x2+ a33· x3+ ⋯ + a3n· xn=c3
⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮   ⋮
    


.
.

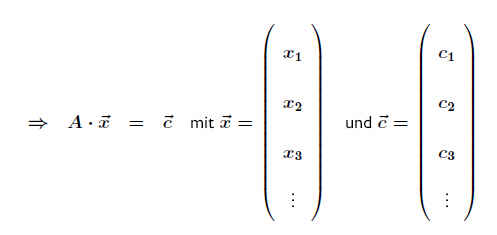Entsprechend verfolgt jetzt der Gaußsche Algorithmus das Ziel, über äquivalente Umformungen die Matrix A in ein gestaffeltes System (Dreiecksform) zu bringen durch die Schritte:

  1. Vertauschen von Zeilen
  2. Multiplikation mit einem Faktor ≠ 0
  3. Addition eines Vielfachen einer anderen Zeile

.
Beispiel 15 - 16 mt9026 .
Lösen eines Gleichungssytems mit Excel : .
.
.

.
.
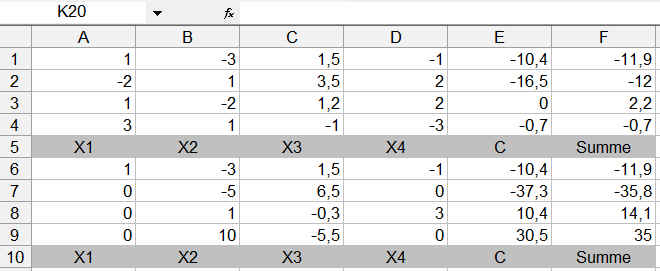Lösung ansehen .
.

.
Beispiel 15 - 17 mt9009 .
Lösung des obigen Beispiels: .
.
.

.
.
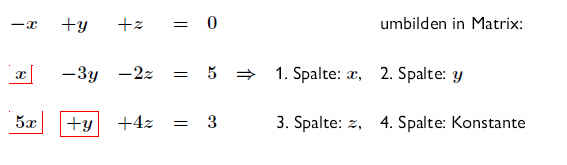Lösung ansehen .
.