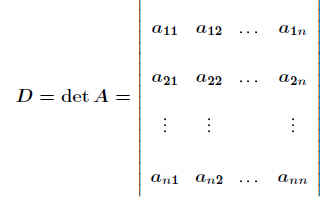16.2.3  Determinanten höherer Ordnung

Für (quadratische!) nxn-Matrizen können Determinanten n-ter Ordnung entsprechend angegeben werden:
.
.

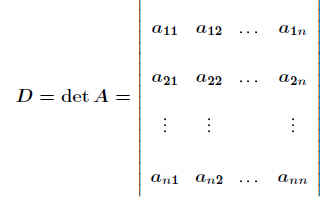Die o.a. Rechenregeln für Determinanten gelten entsprechend.
Die Determinante kann man nach dem Laplaceschen Entwicklungssatz einer nxn-Matrix durch Entwickeln nach einer Zeile oder Spalte berechnen: .
.
D = ∑_k=1ⁿ a_ik · A_ik oder D = ∑_i=1ⁿ a_ik · A_ik . .
.
Die A_ik sind die algebraischen Komplemente von a_ik in D: A_ik = (−1)^i+k · D_ik
Vorgehen bei der Bestimmung einer n-reihigen Determinante:

1. Man versucht, mit Hilfe elementarer Umformungen zunächst die Elemente einer Zeile (oder Spalte) bis auf eines (oder wenigen) auf Null zu bringen.
2. Durch Entwicklung nach diesen Elementen erhält man eine (n-1)-reihige Unterdeterminante.
3. Dies wird solange wiederholt, bis man z.B. 3-reihige Determinanten nach der Regel von Sarrus bestimmen kann. .
   

.
Beispiel 16 - 30 mt9017 .
.
.

.
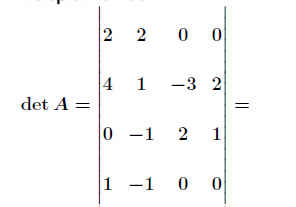Lösung ansehen .
.

.
.
Beispiel 16 - 31 mt9018 .
.
.

.
.
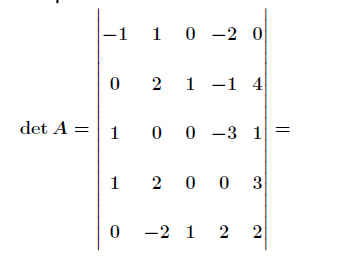Lösung ansehen .
.

.